题目内容
复数z满足条件：|2z+1|=|z-i|，那么z对应的点的轨迹是（ ）
| A、圆 | B、椭圆 | C、双曲线 | D、抛物线 |
考点：复数求模,轨迹方程
专题：数系的扩充和复数
分析：设复数z=x+yi，x，y∈R，由模长公式化简可得．
解答：
解：设复数z=x+yi，x，y∈R，
∵|2z+1|=|z-i|，
∴|2z+1|2=|z-i|2，
∴（2x+1）2+4y2=x2+（y-1）2，
化简可得3x2+3y2+4x+2y=0，
满足42+22-4×3×0=20＞0，表示圆，
故选：A
∵|2z+1|=|z-i|，
∴|2z+1|2=|z-i|2，
∴（2x+1）2+4y2=x2+（y-1）2，
化简可得3x2+3y2+4x+2y=0，
满足42+22-4×3×0=20＞0，表示圆，
故选：A
点评：本题考查复数的模，涉及轨迹方程的求解和圆的方程，属基础题．
练习册系列答案
相关题目
集合A={3，log2a}，B={a，b}，若A∩B={2}，则A∪B=（ ）
| A、{2，3，4} |
| B、{2，4} |
| C、{2，3} |
| D、{1，2，3，4} |
如图所示为一简谐振动的图象，则下列判断正确的是（ ）
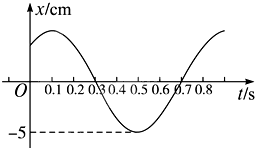
| A、该质点的振动周期为0.7s |
| B、该质点的振幅为5cm |
| C、该质点在0.1s和0.5s时振动速度最大 |
| D、该质点在0.3s和0.7s时的加速度为零 |
已知实数a，b满足a＞b，则下列说法一定正确的是（ ）
| A、a-c＞b-c | ||||
| B、a2＞b2 | ||||
C、
| ||||
| D、ac2＞bc2 |
sin（
-θ）+cos（
-θ）=
，则cos2θ的值为（ ）
| π |
| 4 |
| π |
| 4 |
| 1 |
| 5 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
设△ABC的三个内角A，B，C所对的边分别是a，b，c，已知A=60°，a=
，c=
，则b=（ ）
| 6 |
| 2 |
A、
| ||||
B、
| ||||
C、2
| ||||
| D、3 |
已知sinα=
，则cos4α的值是（ ）
| ||
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
若θ为锐角，求y=3cosθ•sin2θ的最大值是（ ）
| A、3 | ||||
B、
| ||||
C、
| ||||
| D、1 |