题目内容
求函数y=2x2-5x+4的单调区间.
考点:二次函数的性质
专题:数形结合,函数的性质及应用
分析:根据二次函数y=f(x)=2x2-5x+4的图象与性质,即可得出f(x)的单调区间是什么.
解答:
解:∵二次函数y=f(x)=2x2-5x+4的图象是抛物线,
且开口向上,对称轴是x=
;
∴当x>
时,f(x)是单调增函数,
x<
时,f(x)是单调减函数,
∴f(x)的单调减区间是(-∞,
),
单调增区间是(
,+∞).
且开口向上,对称轴是x=
| 5 |
| 4 |
∴当x>
| 5 |
| 4 |
x<
| 5 |
| 4 |
∴f(x)的单调减区间是(-∞,
| 5 |
| 4 |
单调增区间是(
| 5 |
| 4 |
点评:本题考查了二次函数的图象与性质的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设非负实数x,y满足
,则z=3x+2y的最大值是( )
|
| A、7 | B、6 | C、9 | D、12 |
已知f(x)=
,则f(3)=( )
|
| A、3 | B、2 | C、4 | D、5 |
设函数f(x)=3sin(2x+
)(x∈R)的图象为C,则下列表述正确的是( )
| π |
| 4 |
A、点(
| ||
B、直线x=
| ||
C、点(
| ||
D、直线x=
|

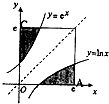 如图,在边长为e(e为自然对数的底数)的正方形区域的A处于C处各有一个通信基站,其信号覆盖范围分别为如图所示的阴影区域.该正方形区域内无其它信号来源且这两个基站工作正常,若在该正方形区域内随机选择一个地点,则该地点无信号的概率为( )
如图,在边长为e(e为自然对数的底数)的正方形区域的A处于C处各有一个通信基站,其信号覆盖范围分别为如图所示的阴影区域.该正方形区域内无其它信号来源且这两个基站工作正常,若在该正方形区域内随机选择一个地点,则该地点无信号的概率为( )