题目内容
 已知梯形ABCD中AD∥BC,∠ABC=∠BAD=
已知梯形ABCD中AD∥BC,∠ABC=∠BAD=| π |
| 2 |
使平面AEFD⊥平面EBCF(如图).G是BC的中点.
(1)当x=2时,求证:BD⊥EG;
(2)当x变化时,求三棱锥D-BCF体积的最大值.
考点:棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:(1)利用面面垂直的性质证线面垂直,由线面垂直⇒线线垂直,再由线线垂直证线面垂直,由线面垂直的性质证得线线垂直;
(2)根据题意先求得棱锥的高,再根据体积公式求三棱锥的体积即可,从而可求三棱锥D-BCF体积的最大值.
(2)根据题意先求得棱锥的高,再根据体积公式求三棱锥的体积即可,从而可求三棱锥D-BCF体积的最大值.
解答:
 (1)证明:作DH⊥EF,垂足H,连结BH,GH,
(1)证明:作DH⊥EF,垂足H,连结BH,GH,
∵平面AEFD⊥平面EBCF,交线EF,DH?平面AEFD,
∴DH⊥平面EBCF,又EG?平面EBCF,故EG⊥DH.
∵EH=AD=
BC=BG,EF∥BC,∠ABC=90°.
∴四边形BGHE为正方形,∴EG⊥BH.
又BH、DH?平面DBH,且BH∩DH=H,故EG⊥平面DBH.
又BD?平面DBH,∴EG⊥BD.
(2)解:∵AE⊥EF,平面AEFD⊥平面EBCF,交线EF,AE?平面AEFD.
∴AE⊥面EBCF.又由(1)DH⊥平面EBCF,故AE∥GH,
∴四边形AEHD是矩形,DH=AE,故以F、B、C、D为顶点的三
棱锥D-BCF的高DH=AE=x.
又S△BCF=
BC•BE=8-2x,(0<x<4).
∴三棱锥D-BCF的体积f(x)=
S△BFC•AE=
(8-2x)x=-
x2+
x,(0<x<4).
∴x=2时,最大值为
.
 (1)证明:作DH⊥EF,垂足H,连结BH,GH,
(1)证明:作DH⊥EF,垂足H,连结BH,GH,∵平面AEFD⊥平面EBCF,交线EF,DH?平面AEFD,
∴DH⊥平面EBCF,又EG?平面EBCF,故EG⊥DH.
∵EH=AD=
| 1 |
| 2 |
∴四边形BGHE为正方形,∴EG⊥BH.
又BH、DH?平面DBH,且BH∩DH=H,故EG⊥平面DBH.
又BD?平面DBH,∴EG⊥BD.
(2)解:∵AE⊥EF,平面AEFD⊥平面EBCF,交线EF,AE?平面AEFD.
∴AE⊥面EBCF.又由(1)DH⊥平面EBCF,故AE∥GH,
∴四边形AEHD是矩形,DH=AE,故以F、B、C、D为顶点的三
棱锥D-BCF的高DH=AE=x.
又S△BCF=
| 1 |
| 2 |
∴三棱锥D-BCF的体积f(x)=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
∴x=2时,最大值为
| 8 |
| 3 |
点评:本题考查线面垂直的性质及棱锥的体积,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
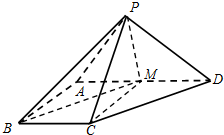 如图,四棱锥P-ABCD中,AB⊥AD,AD∥BC,AD=2,AB=BC=1,PA=PD=
如图,四棱锥P-ABCD中,AB⊥AD,AD∥BC,AD=2,AB=BC=1,PA=PD= 在四棱锥P-ABCD中,地面ABCD为直角梯形,AD∥BC,∠ABC=
在四棱锥P-ABCD中,地面ABCD为直角梯形,AD∥BC,∠ABC=