题目内容
4．已知复数z满足i（z+1）=-2+2i（i是虚数单位）（1）求z的虚部；
（2）若$ω=\frac{z}{1-2i}$，求|ω|2012．
分析 （1）利用复数的运算法则、虚部的定义即可得出．
（2）利用复数的运算法则、几何意义即可得出．
解答 解：（1）∵$i（z+1）=-2+2i∴z+1=\frac{-2+2i}{i}=2+2i$，z=1+2i，z的虚部为2．
（2）$ω=\frac{z}{1-2i}=-\frac{3}{5}+\frac{4}{5}i$，|ω|=1，|ω|2012=1．
点评 本题考查了复数的运算法则、共轭复数的定义、几何意义、虚部的定义，考查了推理能力与计算能力，属于基础题．
练习册系列答案
口算题天天练系列答案
相关题目
6．根据如下样本数据得到的回归方程为$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，若$\stackrel{∧}{a}$=4.5，则x每增加1个单位，y就（ ）
| x | 3 | 4 | 5 | 6 | 7 |
| y | 4 | 2.5 | -0.5 | 0.5 | -2 |
| A． | 增加0.9个单位 | B． | 减少0.9个单位 | C． | 增加0.72个单位 | D． | 减少0.72个单位 |
7．
秦九韶是我国南宋时代的数学家，其代表作《数书九章》是我国13世纪数学成就的代表之一，秦九韶利用其多项式算法，给出了求高次代数方程的完整算法，这一成就比西方同样的算法早五六百年，如图是该算法求函数f（x）=x3+x+1零点的程序框图，若输入x=-1，c=1，d=0.1，则输出的x的值为（ ）
秦九韶是我国南宋时代的数学家，其代表作《数书九章》是我国13世纪数学成就的代表之一，秦九韶利用其多项式算法，给出了求高次代数方程的完整算法，这一成就比西方同样的算法早五六百年，如图是该算法求函数f（x）=x3+x+1零点的程序框图，若输入x=-1，c=1，d=0.1，则输出的x的值为（ ）| A． | -0.6 | B． | -0.69 | C． | -0.7 | D． | -0.71 |
某高校调查了400名大学生每周的自习时间（单位：小时），制成了如图所示的频率分布直方图，其中自习时间的范围是[17.5，30]，样本数据分组为[17.5，20），[20，22.5），[22.5，25）[25，27.5），[27.5，30]．根据此直方图，这400名大学生中每周的自习时间不少于25小时的人数是120．
19．如图所示，在?ABCD中，AE：EB=1：2，若S△AEF=6cm2，则S△CDF为（ ）
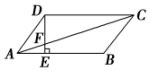
| A． | 54 cm2 | B． | 24 cm2 | C． | 18 cm2 | D． | 12 cm2 |
14．
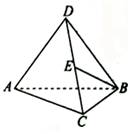如图，在三棱锥D-ABC中，∠ABC=90°，平面DAB⊥平面ABC，DA=AB=DB=BC，E是DC的中点，则AC与BE所成角的余弦值为（ ）
如图，在三棱锥D-ABC中，∠ABC=90°，平面DAB⊥平面ABC，DA=AB=DB=BC，E是DC的中点，则AC与BE所成角的余弦值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{{\sqrt{15}}}{16}$ | D． | $\frac{1}{3}$ |