题目内容
14. 已知函数y=f(x)的图象是折线ABCDE,如图,其中A(1,2),B(2,1),C(3,2),D(4,1),E(5,2),若直线y=kx+b与y=f(x)的图象恰有四个不同的公共点,则k的取值范围是( )
已知函数y=f(x)的图象是折线ABCDE,如图,其中A(1,2),B(2,1),C(3,2),D(4,1),E(5,2),若直线y=kx+b与y=f(x)的图象恰有四个不同的公共点,则k的取值范围是( )| A. | (-1,0)∪(0,1) | B. | $(-\frac{1}{3},\frac{1}{3})$ | C. | (0,1] | D. | $[{0.\frac{1}{3}}]$ |
分析 根据图象使用特殊值验证,使用排除法得出答案.
解答  解;当k=0,1<b<2时,显然直线y=b与f(x)图象交于四点,故k可以取0,排除A,C
解;当k=0,1<b<2时,显然直线y=b与f(x)图象交于四点,故k可以取0,排除A,C
作直线BE,则kBE=$\frac{2-1}{5-2}=\frac{1}{3}$,直线BE与f(x)图象交于三点,
平行移动直线BD可发现直线与f(x)图象最多交于三点,
即直线y=$\frac{1}{3}x+b$与f(x)图象最多交于三点,∴k≠$\frac{1}{3}$.排除D.
故选B.
点评 本题考查了函数图象的交点个数,利用特殊值采用数形结合法可方便解出答案.

练习册系列答案
相关题目
4.根据如样本数据:
得到的回归直线方程为$\widehat{y}$=10.5x+a,据此模型来预测当x=20时,y的值为( )
| x | 2 | 4 | 5 | 6 | 8 |
| y | 20 | 40 | 60 | 70 | 80 |
| A. | 210 | B. | 210.5 | C. | 211.5 | D. | 212.5 |
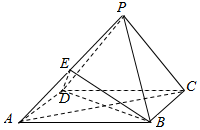 如图,在四棱锥P-ABCD中,底面为矩形,平面PCD丄平面ABCD,PC丄PD,PD=AD,E为PA的中点.
如图,在四棱锥P-ABCD中,底面为矩形,平面PCD丄平面ABCD,PC丄PD,PD=AD,E为PA的中点.