题目内容
3.已知偶函数f(x)在(-∞,0]单调递减,f(1)=0.若f(lgx)<0,则x的取值范围是($\frac{1}{10}$,10).分析 根据条件可以得出偶函数f(x)在[0,+∞)上单调递增,并且f(1)=0,从而由f(lgx)<0便可得出|lgx|<1,解该不等式便可得出x的取值范围.
解答 解:偶函数f(x)在(-∞,0]上单调递减;
∴f(x)在[0,+∞)上单调递增,又f(1)=0;
∴由f(lgx)<0得,f(|lgx|)<f(1);
∴|lgx|<1;
∴-1<lgx<1;
∴$\frac{1}{10}<x<10$;
∴x的取值范围是$(\frac{1}{10},10)$.
故答案为:$(\frac{1}{10},10)$.
点评 考查偶函数的定义,偶函数在对称区间上的单调性特点,以及对数函数的单调性,绝对值不等式的解法.

练习册系列答案
相关题目
14. 已知函数y=f(x)的图象是折线ABCDE,如图,其中A(1,2),B(2,1),C(3,2),D(4,1),E(5,2),若直线y=kx+b与y=f(x)的图象恰有四个不同的公共点,则k的取值范围是( )
已知函数y=f(x)的图象是折线ABCDE,如图,其中A(1,2),B(2,1),C(3,2),D(4,1),E(5,2),若直线y=kx+b与y=f(x)的图象恰有四个不同的公共点,则k的取值范围是( )
 已知函数y=f(x)的图象是折线ABCDE,如图,其中A(1,2),B(2,1),C(3,2),D(4,1),E(5,2),若直线y=kx+b与y=f(x)的图象恰有四个不同的公共点,则k的取值范围是( )
已知函数y=f(x)的图象是折线ABCDE,如图,其中A(1,2),B(2,1),C(3,2),D(4,1),E(5,2),若直线y=kx+b与y=f(x)的图象恰有四个不同的公共点,则k的取值范围是( )| A. | (-1,0)∪(0,1) | B. | $(-\frac{1}{3},\frac{1}{3})$ | C. | (0,1] | D. | $[{0.\frac{1}{3}}]$ |
18.若tan(180°-α)=-$\frac{4}{3}$,则tan(α+405°)等于( )
| A. | $\frac{1}{7}$ | B. | 7 | C. | -$\frac{1}{7}$ | D. | -7 |
12.已知$\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$,$\overrightarrow{AE}$=$\frac{2}{3}$$\overrightarrow{AC}$,$\overrightarrow{DE}$等于( )
| A. | $\frac{1}{3}$$\overrightarrow{CB}$ | B. | -$\frac{1}{3}$$\overrightarrow{CB}$ | C. | -$\frac{2}{3}$$\overrightarrow{CB}$ | D. | $\frac{2}{3}$$\overrightarrow{CB}$ |
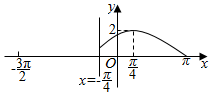 已知定义在区间[-$\frac{3π}{2}$,π]上的函数y=f(x)的图象关于直线x=-$\frac{π}{4}$对称,当x∈[-$\frac{π}{4}$,π]时,函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$),且其图象如图所示.
已知定义在区间[-$\frac{3π}{2}$,π]上的函数y=f(x)的图象关于直线x=-$\frac{π}{4}$对称,当x∈[-$\frac{π}{4}$,π]时,函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$),且其图象如图所示.