题目内容
如图,已知平行六面体ABCD—A1B1C1D1的底面为正方形,O1、O分别为上、下底面的中心,且A1在底面ABCD上的射影是O。
(1)求证:平面O1DC⊥平面ABCD;
(2)若∠A1AB=60°,求平面BAA1与平面CAA1的夹角的余弦值。
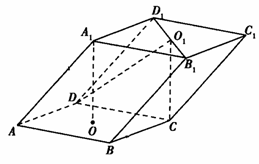
(1)连结AC,BD,AC,则O为AC,BD的交点O1为A1C1,B1D1的交点。
由平行六面体的性质知:A1O1∥OC且A1O1=OC,
 四边形A1OCO1为平行四边形, ………(2分)
四边形A1OCO1为平行四边形, ………(2分)
 A1O∥O1C. 又∵A1O⊥平面ABCD,
A1O∥O1C. 又∵A1O⊥平面ABCD,
 O1C⊥平面ABCD, ………(4分)
O1C⊥平面ABCD, ………(4分)
又∵O1C 平面O1DC,
平面O1DC,
 平面O1DC⊥平面ABCD。 ………(6分)
平面O1DC⊥平面ABCD。 ………(6分)
(2)由题意可知Rt A1OB≌Rt
A1OB≌Rt A1OA,则A1A=A1B,
A1OA,则A1A=A1B,
又∠A1AB=600,故 A1AB是等边三角形。 …………(7分)
A1AB是等边三角形。 …………(7分)
不妨设AB=a, 则在Rt A1OA中,OA=
A1OA中,OA= a, AA1=a, OA1=
a, AA1=a, OA1= a,
a,
如图分别以OB,OC,OA1为x轴,y轴,z轴建立空间直角坐标系,
则可得坐标为A(0,- a,0), B(
a,0), B( a,0,0), A1(0,0,,
a,0,0), A1(0,0,, a) …………(8分)
a) …………(8分)
 =(
=( a,
a, a,0),
a,0),  =(-
=(- a,0,
a,0, a)
a)
设平面ABA1的法向量为 =(x,y,z)
=(x,y,z)
则由 ·
· =0得x+y=0,由
=0得x+y=0,由 ·
· =0得x-z=0
=0得x-z=0
令x=1得 =(1,-1,1) …………(10分)
=(1,-1,1) …………(10分)
又知BD⊥平面ACC1A1,故可得平面CAA1的一个法向量为 =(1,0,0)
=(1,0,0)
cosθ=| |=
|=
从而平面BAA1与平面CAA1的夹角的余弦值为 。 …………(12分)
。 …………(12分)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点(1, 2)在“上”区域内,则双曲线离心率的取值范围为 。
的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点(1, 2)在“上”区域内,则双曲线离心率的取值范围为 。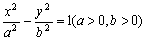 的左焦点为F1,左、右顶点分别为A1、A2,
的左焦点为F1,左、右顶点分别为A1、A2,
 (t∈R),它们的交点坐标为 。
(t∈R),它们的交点坐标为 。 C.98 D.49
C.98 D.49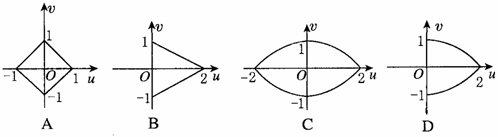
 则f′(x)
则f′(x) 的解集为 ( )
的解集为 ( ) B.(-1,0)
B.(-1,0) C.
C. D.
D.
 ,则
,则 ( )
( ) B.
B. C.
C. D.
D. 