题目内容
(附加题)本题满分20分
如图,已知抛物线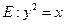
 与圆
与圆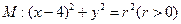 相交于A、B、C、D四个点。
相交于A、B、C、D四个点。
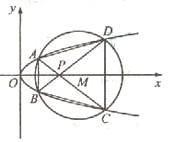
(Ⅰ)求r的取值范围 (Ⅱ)当四边形ABCD的面积最大时,求对角线AC、BD的交点P的坐标。
如图,已知抛物线
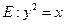
 与圆
与圆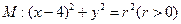 相交于A、B、C、D四个点。
相交于A、B、C、D四个点。
(Ⅰ)求r的取值范围 (Ⅱ)当四边形ABCD的面积最大时,求对角线AC、BD的交点P的坐标。
(1)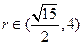 (2)
(2)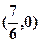
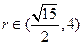 (2)
(2)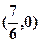
(Ⅰ)将抛物线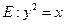 代入圆
代入圆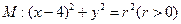 的方程,消去
的方程,消去 ,整理得
,整理得 .............(1)
.............(1)
抛物线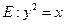 与圆
与圆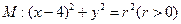 相交于
相交于 、
、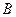 、
、 、
、 四个点的充要条件是:方程(1)有两个不相等的正根
四个点的充要条件是:方程(1)有两个不相等的正根
∴
 即{
即{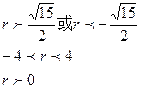
 解这个不等式组得
解这个不等式组得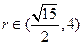 .
.
(II) 设四个交点的坐标分别为 、
、 、
、 、
、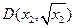 。则直线AC、BD的方程分别为
。则直线AC、BD的方程分别为

解得点P的坐标为 。则由(I)根据韦达定理有
。则由(I)根据韦达定理有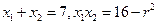 ,
,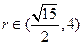 由于四边形ABCD为等腰梯形,因而其面积
由于四边形ABCD为等腰梯形,因而其面积
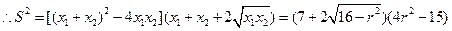
令 ,则
,则 下面求
下面求 的最大值。
的最大值。
方法1:由三次均值有:


当且仅当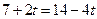 ,即
,即 时取最大值。经检验此时
时取最大值。经检验此时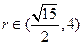 满足题意。故所求的点P的坐标为
满足题意。故所求的点P的坐标为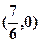
法2:令 ,
, ,
,
∴ ,
,
令 得
得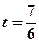 ,或
,或 (舍去)
(舍去)
当 时,
时, ;当
;当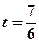 时
时 ;当
;当 时,
时,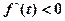
故当且仅当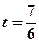 时,
时,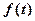 有最大值,即四边形ABCD的面积最大,故所求的点P的坐标为
有最大值,即四边形ABCD的面积最大,故所求的点P的坐标为
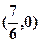
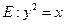 代入圆
代入圆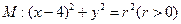 的方程,消去
的方程,消去 ,整理得
,整理得 .............(1)
.............(1)抛物线
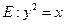 与圆
与圆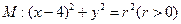 相交于
相交于 、
、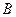 、
、 、
、 四个点的充要条件是:方程(1)有两个不相等的正根
四个点的充要条件是:方程(1)有两个不相等的正根∴

 即{
即{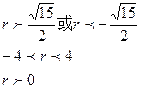
 解这个不等式组得
解这个不等式组得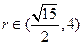 .
. (II) 设四个交点的坐标分别为
 、
、 、
、 、
、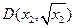 。则直线AC、BD的方程分别为
。则直线AC、BD的方程分别为 
解得点P的坐标为
 。则由(I)根据韦达定理有
。则由(I)根据韦达定理有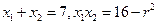 ,
,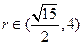 由于四边形ABCD为等腰梯形,因而其面积
由于四边形ABCD为等腰梯形,因而其面积
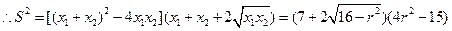
令
 ,则
,则 下面求
下面求 的最大值。
的最大值。方法1:由三次均值有:


当且仅当
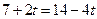 ,即
,即 时取最大值。经检验此时
时取最大值。经检验此时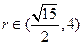 满足题意。故所求的点P的坐标为
满足题意。故所求的点P的坐标为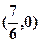
法2:令
 ,
, ,
,∴
 ,
, 令
 得
得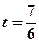 ,或
,或 (舍去)
(舍去)当
 时,
时, ;当
;当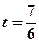 时
时 ;当
;当 时,
时,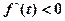
故当且仅当
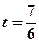 时,
时,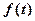 有最大值,即四边形ABCD的面积最大,故所求的点P的坐标为
有最大值,即四边形ABCD的面积最大,故所求的点P的坐标为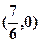

练习册系列答案
相关题目

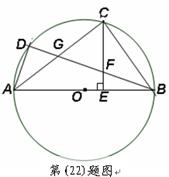
 是
是 的直径,
的直径, ,
, 是
是 于
于 ,
, 交
交 于
于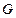 ,交
,交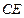 于
于 ,
, .
.
 的中点;
的中点; .
.
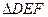 ~
~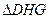 ;
;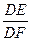 的值。
的值。
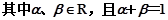 ,则点C的轨迹方程是( )
,则点C的轨迹方程是( )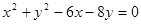 ,过点
,过点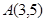 的直线被圆所截,则截得的最短弦的长度为
的直线被圆所截,则截得的最短弦的长度为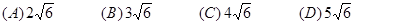
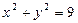 外一点
外一点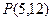 引圆的割线交圆于
引圆的割线交圆于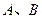 两点,求弦
两点,求弦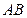 的中点
的中点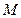 的轨迹方程。
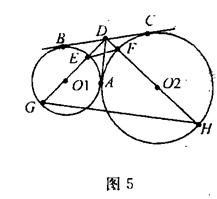
的轨迹方程。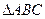 中,
中,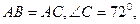 ⊙
⊙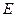 过
过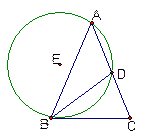
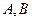 两点且与
两点且与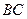 相切于点
相切于点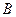 ,与
,与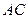 交于点
交于点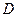 ,连结
,连结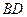 ,
,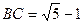 ,则
,则
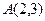 的直线的参数方程为
的直线的参数方程为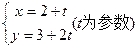 ,若此直线与直线
,若此直线与直线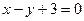 相较于点
相较于点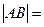
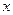 的不等式
的不等式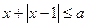 无解,则实数
无解,则实数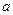 的取值范围为
的取值范围为 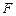 (0,1),并且与直线
(0,1),并且与直线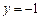 相切,若直线
相切,若直线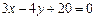 与圆C有公共点,则圆C的面积
与圆C有公共点,则圆C的面积