题目内容
给定k∈N*,设函数f:N*→N*满足:对于任意大于k的正整数n,f(n)=n-k.
(1)设k=1,则其中一个函数f在n=1处的函数值为________.
(2)设k=4,且当n≤4时,2≤f(n)≤3,则不同的函数f的个数为________.
(1)a(a为正整数) (2)16
(2)解析 (1)本题定义函数有两个条件,一是定义域和值域都是正整数,二是对于任意大于k的正整数n,f(n)=n-k.那么n=1时只要满足值域是正整数即可,所以答案是a(a为正整数).
(2)因为k=4,所以n>4时都一一对应,只要对n≤4的进行定义,又因为f(n)=2或f(n)=3,所以f(1)=2或3,f(2)=2或3,f(3)=2或3,f(4)=2或3,所以f的个数为:2×2×2×2=16.

练习册系列答案
相关题目
 与直线
与直线 关于点
关于点 对称,则
对称,则 ________.
________.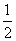 ”的( )
”的( ) 若f(a)+f(1)=0,则实数a的值等于( )
若f(a)+f(1)=0,则实数a的值等于( ) φ(x)=
φ(x)= 则当x<0时,f(φ(x))=________.
则当x<0时,f(φ(x))=________.
 的定义域是( )
的定义域是( )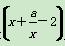 ,其中a是大于0的常数.
,其中a是大于0的常数. B.xa>xb
B.xa>xb