题目内容
14.已知实数x,y满足$\left\{\begin{array}{l}{x-y≤0}\\{x+y-5≥0}\\{y≤3}\end{array}\right.$,若不等式$\frac{(x+y)^2}{x^2+y^2}$≥a恒成立,则实数a的最大值为( )| A. | 1 | B. | $\frac{2}{3}$ | C. | $\frac{25}{13}$ | D. | 2 |
分析 由约束条件作出可行域,求出$\frac{y}{x}$的范围,由$\frac{(x+y)^2}{x^2+y^2}$=$1+\frac{2\frac{y}{x}}{1+(\frac{y}{x})^{2}}$=$1+\frac{2}{\frac{y}{x}+\frac{1}{\frac{y}{x}}}$,求出其范围,可得使不等式$\frac{(x+y)^2}{x^2+y^2}$≥a恒成立的实数a的最大值.
解答 解:由约束条件$\left\{\begin{array}{l}{x-y≤0}\\{x+y-5≥0}\\{y≤3}\end{array}\right.$作出可行域如图,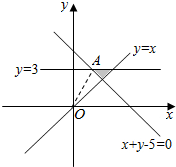
∵$\frac{(x+y)^2}{x^2+y^2}$=$\frac{{x}^{2}+{y}^{2}+2xy}{{x}^{2}+{y}^{2}}=1+\frac{2xy}{{x}^{2}+{y}^{2}}$=$1+\frac{2\frac{y}{x}}{1+(\frac{y}{x})^{2}}$=$1+\frac{2}{\frac{y}{x}+\frac{1}{\frac{y}{x}}}$,
设z=$\frac{y}{x}$,
由图可知,1$<z<\frac{3}{2}$,
∴z$+\frac{1}{z}$∈(2,$\frac{13}{6}$),则$\frac{2}{z+\frac{1}{z}}∈(\frac{12}{13},1)$,
∴$\frac{(x+y)^2}{x^2+y^2}$∈($\frac{25}{13},2$).
∵不等式$\frac{(x+y)^2}{x^2+y^2}$≥a恒成立,
∴$a≤\frac{25}{13}$.
故选:C.
点评 本题考查简单的线性规划,考查了数学转化思想方法,训练了恒成立问题的求法,是中档题.

| A. | (0,1) | B. | (0,3) | C. | (1,+∞) | D. | (1,3) |
| A. | $\sqrt{10}$ | B. | 10 | C. | $\sqrt{5}$ | D. | 3 |