题目内容
2．已知p：2a≤x≤a2+1，q：x2-3（a+1）x+6a+2≤0，若p是q的充分条件，求实数a取值范围．分析 设A={x|2a≤x≤a2+1}，B={x|（x-2）[x-（3a+1）]≤0}，由于p是q的充分条件，可得A⊆B．
（1）当a≥$\frac{1}{3}$时，此时B={x|2≤x≤3a+1}，可得$\left\{\begin{array}{l}{2a≥2}\\{{a}^{2}+1≤3a+1}\end{array}\right.$．
（2）当a＜$\frac{1}{3}$时，B={x|3a+1≤x≤2}，可得$\left\{\begin{array}{l}{2a≥3a+1}\\{{a}^{2}+1≤2}\end{array}\right.$．
解答 解：x2-3（a+1）x+6a+2≤0，化为（x-2）[x-（3a+1）]≤0，
设A={x|2a≤x≤a2+1}，B={x|（x-2）[x-（3a+1）]≤0}，∵p是q的充分条件，∴A⊆B．
（1）当a≥$\frac{1}{3}$时，B={x|2≤x≤3a+1}，∴$\left\{\begin{array}{l}{2a≥2}\\{{a}^{2}+1≤3a+1}\end{array}\right.$，解得1≤a≤3．
（2）当a＜$\frac{1}{3}$时，B={x|3a+1≤x≤2}，∴$\left\{\begin{array}{l}{2a≥3a+1}\\{{a}^{2}+1≤2}\end{array}\right.$，解得a=-1．
∴实数a取值范围是{a|1≤a≤3，或a=-1}．
点评 本题考查了不等式的性质、简易逻辑的判定方法、集合的运算性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
12．化简$\frac{1}{\sqrt{1+ta{n}^{2}160°}}$的结果为（ ）
| A． | -cos160° | B． | cos160° | C． | $\frac{1}{cos160°}$ | D． | $\frac{1}{-cos160°}$ |
13．甲口袋内有大小相等的2个红球和3个白球，乙口袋内装有大小相等的1个红球和2个白球，从两个口袋中各摸出1个球，那么$\frac{7}{15}$等于（ ）
| A． | 2个球都是白球的概率 | B． | 2个球中恰好有1个是白球的概率 | ||
| C． | 2个球都不是白球的概率 | D． | 2个球至少有一个白球的概率 |
10．函数y=sin2x（x∈[-$\frac{π}{8}$，$\frac{2π}{3}$]）的单调递减区间是（ ）
| A． | [$\frac{π}{4}$，$\frac{2π}{3}$] | B． | [-$\frac{π}{8}$，$\frac{π}{4}$] | C． | [-$\frac{π}{8}$，$\frac{2π}{3}$] | D． | [0，$\frac{2π}{3}$] |
17．已知集合A={1，2，3，4，5}，B={x|x＜2}，则A∩B等于（ ）
| A． | {1} | B． | {1，2} | C． | {1，2，3} | D． | {1，2，3，4} |
14．已知实数x，y满足$\left\{\begin{array}{l}{x-y≤0}\\{x+y-5≥0}\\{y≤3}\end{array}\right.$，若不等式$\frac{（x+y）^2}{x^2+y^2}$≥a恒成立，则实数a的最大值为（ ）
| A． | 1 | B． | $\frac{2}{3}$ | C． | $\frac{25}{13}$ | D． | 2 |
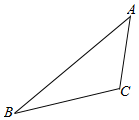在△ABC中，AC=$\sqrt{2}$，AB=$\sqrt{3}$+1，∠BAC=45°，点P满足：$\overrightarrow{BP}$=（1-λ）$\overrightarrow{BA}$+λ$\overrightarrow{BC}$（λ＞0），AP=$\frac{\sqrt{2}}{2}$．
12．y=cos（2x+$\frac{π}{6}$）的最小正周期是（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{π}{2}$ | C． | π | D． | 2π |