题目内容
18.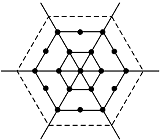 如图所示是一个有n层(n≥2,n∈N*)的六边形点阵,它的中心是一个点,算作第1层,第2层每边有2个点,第3层每边有3个点,…,第n层每边有n个点,则这个点阵共有( )个点.
如图所示是一个有n层(n≥2,n∈N*)的六边形点阵,它的中心是一个点,算作第1层,第2层每边有2个点,第3层每边有3个点,…,第n层每边有n个点,则这个点阵共有( )个点.| A. | n2 | B. | n2+n | C. | 3n2-3n+1 | D. | 3n2-3n |
分析 分析可知规律,从第二层开始,每增加一层就增加六个点,即可得出结论.
解答 解:观察点阵中各层点数的规律,然后归纳出点阵共有的点数.
第一层有点数:1;
第二层有点数:1×6;
第三层有点数:2×6;
第四层有点数:3×6;
…
第n层有点数:(n-1)×6.
因此,这个点阵的第n层有点(n-1)×6个,n层共有点数为
1+1×6+2×6+3×6+…+(n-1)×6
=1+6×[1+2+3+…+(n-1)]
=1+6×$\frac{(n-1)n}{2}$
=1+3(n-1)n=3n2-3n+1.
故选:C.
点评 本题主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.通过分析找到各部分的变化规律后直接利用规律求解.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
13.从0,8中任取一数,从3,5,7中任取两个数字组成无重复数字的三位数,其中奇数的个数为( )
| A. | 24 | B. | 18 | C. | 12 | D. | 6 |
3.下列推理中属于类比推理的是( )
| A. | 一切偶数都能被2整除,2100是偶数,所以2100能被2整除. | |
| B. | 由a1,a2,a3…,归纳出数列的通项公式an | |
| C. | 由平面三角形的性质,推测空间四边形的性质 | |
| D. | 如果a>b,c>d,则a-d>b-c |
7.如图所示的程序框图,输出的S的值为( )
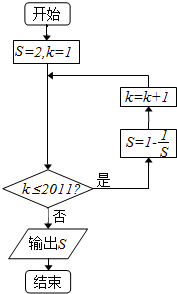

| A. | $\frac{1}{2}$ | B. | 2 | C. | -1 | D. | -$\frac{1}{2}$ |
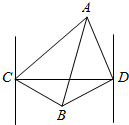 如图,一轮船自西向东匀速行驶,在C处测得A岛在东北方向,B岛在南偏东60°方向,此船向东航行6000海里后到达D处,测得A岛在北偏西15°方向,B岛在南偏西75°方向,则A,B两岛间距离为1000$\sqrt{42}$海里(结果保留根号).
如图,一轮船自西向东匀速行驶,在C处测得A岛在东北方向,B岛在南偏东60°方向,此船向东航行6000海里后到达D处,测得A岛在北偏西15°方向,B岛在南偏西75°方向,则A,B两岛间距离为1000$\sqrt{42}$海里(结果保留根号).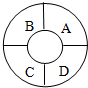 有4种不同的备选颜色给如图示的A、B、C、D四块涂色,要求每块涂同一种颜色,且相邻两块涂不同的颜色,则不同的涂色方法有( )种.
有4种不同的备选颜色给如图示的A、B、C、D四块涂色,要求每块涂同一种颜色,且相邻两块涂不同的颜色,则不同的涂色方法有( )种.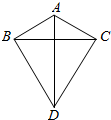 如图,在△ABC中,AB=AC=a,以BC为边向外作正三角形BCD,则AD的最大值为2a.
如图,在△ABC中,AB=AC=a,以BC为边向外作正三角形BCD,则AD的最大值为2a.