题目内容
14.△ABC的三角形A,B,C所对三边分别是a,b,c,B=60°,cosC=$\frac{4}{5}$,b=$\sqrt{3}$,则sinA=$\frac{3+4\sqrt{3}}{10}$.分析 根据同角的三角函数的关系,以及诱导公式,两角和的正弦公式计算即可.
解答 解:在△ABC中,∵cosC=$\frac{4}{5}$,
∴sinC=$\frac{3}{5}$,
∵B=60°,
∴sinA=sin(B+C)=sinCcosB+cosCsinB=$\frac{3}{5}$×$\frac{1}{2}$+$\frac{4}{5}$×$\frac{\sqrt{3}}{2}$=$\frac{3+4\sqrt{3}}{10}$
故答案为:$\frac{3+4\sqrt{3}}{10}$
点评 本题考查了同角的三角函数的关系,以及诱导公式,两角和的正弦公式,属于基础题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
4.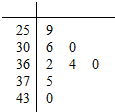 雾霾天气对我们身体影响巨大,据统计我市2015年12月份某8天的空气质量指数(AQI)茎叶统计图如图,则该组数据的中位数为( )
雾霾天气对我们身体影响巨大,据统计我市2015年12月份某8天的空气质量指数(AQI)茎叶统计图如图,则该组数据的中位数为( )
 雾霾天气对我们身体影响巨大,据统计我市2015年12月份某8天的空气质量指数(AQI)茎叶统计图如图,则该组数据的中位数为( )
雾霾天气对我们身体影响巨大,据统计我市2015年12月份某8天的空气质量指数(AQI)茎叶统计图如图,则该组数据的中位数为( )| A. | 360 | B. | 361 | C. | 362 | D. | 363 |