题目内容
已知
=(2,-1,3),
=(-1,4,-2),
=(4,5,x),若
、
、
三向量共面,则|
|=( )
| a |
| b |
| c |
| a |
| b |
| c |
| c |
| A、5 | ||
| B、6 | ||
C、
| ||
D、
|
考点:共线向量与共面向量
专题:空间向量及应用
分析:根据所给的三个向量的坐标,写出三个向量共面的条件,点的关于要求的两个方程组,解方程组即可.
解答:
解:∵
=(2,-1,3),
=(-1,4,-2),
=(4,5,x),
、
、
三向量共面,
∴
=m
+n
∴(2,-1,3)=m(-1,4,-2)+n(4,5,x),
∴
解得,x=5,
则
=(4,5,5),
故|
|=
=
.
故选:C.
| a |
| b |
| c |
| a |
| b |
| c |
∴
| a |
| b |
| c |
∴(2,-1,3)=m(-1,4,-2)+n(4,5,x),
∴
|
解得,x=5,
则
| c |
故|
| c |
| 42+52+52 |
| 66 |
故选:C.
点评:本题考查空间向量的共线向量和共面向量,本题解题的关键是写出三个向量之间的关系,转化成解方程组的问题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
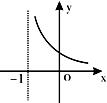
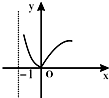
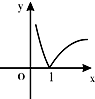
下列所示的图形中,可以作为函数y=f(x)的图象的是( )
A、 |
B、 |
C、 |
D、 |
角θ满足条件sin2θ>0,且cosθ+sinθ>0,则θ在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
f(x)=(a+2b)x+2a-b(a≥0),且当x∈[0,1]时恒有f(x)≤1,则f(-1)的最大值为( )
| A、3 | B、-3 | C、6 | D、-6 |
已知复数z=
(i是虚数单位),则z的共轭复数
=( )
| 2 |
| 1-i |
. |
| z |
| A、1+i | B、1-i |
| C、-1+i | D、-1-i |
阅读如图所示程序:

若输出y=9,则输入的x值应该是( )

若输出y=9,则输入的x值应该是( )
| A、-1 | B、4或-1 |
| C、4 | D、2或-2 |