题目内容
 下表给出了从某校500名12岁男生中用简单随机抽样得出的120人的身高资料(单位:厘米):
下表给出了从某校500名12岁男生中用简单随机抽样得出的120人的身高资料(单位:厘米):| 分组 | 人数 | 频率 |
| [122,126 ) | 5 | 0.042 |
| [126,130) | 8 | 0.067 |
| [130,134 ) | 10 | 0.083 |
| [134,138) | 22 | 0.183 |
| [138,142) | y | |
| [142,146) | 20 | 0.167 |
| [146,150) | 11 | 0.092 |
| [150,154) | x | 0.050 |
| [154,158) | 5 | 0.042 |
| 合计 | 120 | 1.00 |
(2)求表中x与y的值,画出频率分布直方图;
(3)试计算身高在147~152cm的总人数约有多少?
考点:频率分布直方图,频率分布表
专题:概率与统计
分析:(1)根据数据总体的定义及已知中从某校500名12岁男生中用简单随机抽样得出的120人的身高资料进行调查,我们易得到结论.根据各组的频率和为1,及频率=频数÷样本容量,可计算出x,y的值.
(2)由已知条件能作画出频率分布直方图.
(3)根据147~152cm范围内各组的频率,能计算身高在147~152cm的总人数.
(2)由已知条件能作画出频率分布直方图.
(3)根据147~152cm范围内各组的频率,能计算身高在147~152cm的总人数.
解答:
解:(1)在这个问题中,总体是某校500名12岁男生身高,
∵样本容量为120,
[150,154)这一组的频率为0.050,
故x=120×0.050=6,
由于各组的频率和为1,
故y=1-(0.042+0.067+0.083+0.183+0.167+0.092+0.050+0.042)=0.275.
(2)由(1)知x=6,y=0.275.
由题意,画出频率分布直方图如下:
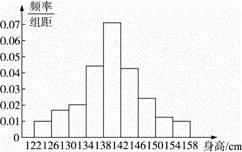
(3)身高在147~152cm的总人数约有:
500(0.092×
+0.050×
)=47(人),
∴身高在147~的总人数约为47人.
∵样本容量为120,
[150,154)这一组的频率为0.050,
故x=120×0.050=6,
由于各组的频率和为1,
故y=1-(0.042+0.067+0.083+0.183+0.167+0.092+0.050+0.042)=0.275.
(2)由(1)知x=6,y=0.275.
由题意,画出频率分布直方图如下:

(3)身高在147~152cm的总人数约有:
500(0.092×
| 3 |
| 4 |
| 1 |
| 2 |
∴身高在147~的总人数约为47人.
点评:本题考查的知识点是频率分布直言图及折线图,频率分布直方表,其中频率=频数÷样本容量=矩形的高×组矩是解答此类问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知a3+a2<0,那么a,a2,-a,-a2的大小关系是( )
| A、a2>-a>a>-a2 |
| B、-a>a2>a>-a2 |
| C、a2>-a2>a>-a |
| D、a2>-a2>-a>a |
已知A是双曲线
-
=1(a>0,b>0)的左顶点,F1、F2分别为双曲线的左、右焦点,P为双曲线上一点,G是△PF1F2的重心,若
=λ
,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| GA |
| PF1 |
| A、3 | B、2 |
| C、4 | D、与λ的取值有关 |
已知正三角形OAB中,点O为原点,点B的坐标是(-3,4),点A在第一象限,向量
=(-1,0),记向量
与向量
的夹角为α,则sinα的值为( )
| m |
| m |
| OA |
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,已知A=105°,B=30°,b=2
,则c等于( )
| 2 |
| A、2 | ||
B、2
| ||
| C、4 | ||
D、4
|