题目内容
6.已知复数z=$\frac{{{{({1+i})}^2}-2({1-i})}}{i-3}$,若z2+az+b=1+2i,(1)求|z|;
(2)求实数a,b的值.
分析 (1)直接利用复数代数形式的乘法运算化简,再根据复数模的定义即可求出
(2)根据复数相等的条件得到关于a,b的方程组,解得即可.
解答 (本小题满分10分)
解:(1)$z=\frac{2i-2+2i}{i-3}=\frac{-2+4i}{i-3}=1-i$,∴$|z|=\sqrt{2}$….(5分)
(2)把z=1-i代入z2+az+b=1+2i,即(1-i)2+a(1-i)+b=1+2i,
得a+b-(2+a)i=1+2i,
所以$\left\{\begin{array}{l}a+b=1\\-(2+a)=2\end{array}\right.$,解得a=-4;b=5,
所以实数a,b的值分别为-4,5. ….(10分)
点评 本题考查了复数代数形式的乘法运算,以及复数相等,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列说法正确是( )
| A. | 常数列一定是等比数列 | B. | 常数列一定是等差数列 | ||
| C. | 等比数列一定不是摆动数列 | D. | 等差数列可能是摆动数列 |
11.已知向量$\overrightarrow{a}$=(3,4),则与$\overrightarrow{a}$方向相同的单位向量是( )
| A. | ($\frac{4}{5}$,$\frac{3}{5}$) | B. | ($\frac{3}{5}$,$\frac{4}{5}$) | C. | (-$\frac{3}{5}$-,$\frac{4}{5}$) | D. | (4,3) |
18.设集合A={x|-1≤x≤2},B={x|x<1且x∈Z},则A∩B=( )
| A. | {-1} | B. | {0} | C. | {-1,0} | D. | {0,1} |
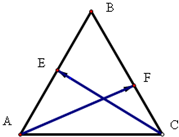 在边长为1的正三角形ABC中,已知$\overrightarrow{AC}=\overrightarrow a,\overrightarrow{AB}$=$\overrightarrow b$,点E线段AB的中点,点F线段BC上,$\overrightarrow{BF}=\frac{2}{3}\overrightarrow{BC}$.
在边长为1的正三角形ABC中,已知$\overrightarrow{AC}=\overrightarrow a,\overrightarrow{AB}$=$\overrightarrow b$,点E线段AB的中点,点F线段BC上,$\overrightarrow{BF}=\frac{2}{3}\overrightarrow{BC}$.