题目内容
17.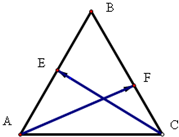 在边长为1的正三角形ABC中,已知$\overrightarrow{AC}=\overrightarrow a,\overrightarrow{AB}$=$\overrightarrow b$,点E线段AB的中点,点F线段BC上,$\overrightarrow{BF}=\frac{2}{3}\overrightarrow{BC}$.
在边长为1的正三角形ABC中,已知$\overrightarrow{AC}=\overrightarrow a,\overrightarrow{AB}$=$\overrightarrow b$,点E线段AB的中点,点F线段BC上,$\overrightarrow{BF}=\frac{2}{3}\overrightarrow{BC}$.(1)以$\overrightarrow a,\overrightarrow b$为基底表示$\overrightarrow{AF},\overrightarrow{CE}$;
(2)求$\overrightarrow{AF}•\overrightarrow{CE}$.
分析 (1)根据平面向量的基本定理进行化简即可,
(2)根据向量数量积的应用进行化简即可.
解答 解:(1)$\overrightarrow{AF}$=$\overrightarrow{AB}$+$\overrightarrow{BF}$=$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{BC}$=$\overrightarrow{AB}$+$\frac{2}{3}$($\overrightarrow{AC}$-$\overrightarrow{AB}$)=$\frac{2}{3}$$\overrightarrow{AC}$+$\frac{1}{3}$$\overrightarrow{AB}$=$\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$;
$\overrightarrow{CE}$=$\frac{1}{2}$($\overrightarrow{CA}$+$\overrightarrow{CB}$)=$-\frac{1}{2}$$\overrightarrow{AC}$+$\frac{1}{2}$($\overrightarrow{AB}$-$\overrightarrow{AC}$)=$\frac{1}{2}$$\overrightarrow{AB}$-$\overrightarrow{AC}$=-$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$;
即$\overrightarrow{AF}=\frac{2}{3}\overrightarrow a+\frac{1}{3}\overrightarrow b,\overrightarrow{CE}=-\overrightarrow a+\frac{1}{2}\overrightarrow b$;
(2)$\overrightarrow{AF}•\overrightarrow{CE}$=($\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$)•(-$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$)=-$\frac{2}{3}$$\overrightarrow{a}$2+$\frac{1}{6}$$\overrightarrow{b}$2=-$\frac{2}{3}$+$\frac{1}{6}$=-$\frac{1}{2}$,
即$\overrightarrow{AF}•\overrightarrow{CE}=-\frac{1}{2}$.
点评 本题主要考查平面向量的基本定理的应用以及向量数量积的应用,比较基础.


| A. | 8 | B. | 30 | C. | 92 | D. | 96 |
| A. | (2,-6) | B. | (-4,-2) | C. | (4,2) | D. | (-4,2) |
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |