题目内容
已知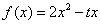 ,且
,且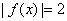 有且仅有两个不同的实根
有且仅有两个不同的实根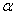 和
和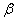 (
( ).
).
(1) 求实数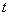 的取值范围;
的取值范围;
(2) 若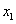 、
、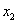

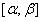 且
且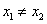 ,求证:
,求证: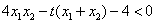 ;
;
(3) 设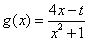 ,对于任意
,对于任意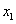 、
、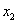

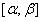 上恒有
上恒有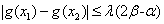 成立,
成立,
求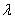 的取值范围.
的取值范围.
解: 1) 根据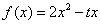 图像 翻折后 顶点值
图像 翻折后 顶点值 ,得
,得 ……….4分
……….4分
2)由韦达定理知 ,不妨设
,不妨设
解1:由于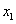 、
、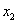

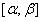 ,故
,故 ,
,
即

 ,
,
解2: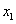 、
、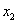

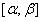 ,且
,且 函数开口朝上,故
函数开口朝上,故 ,两式相加,利用基本不等式
,两式相加,利用基本不等式
3) ,所以
,所以
任取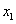 、
、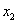

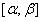 ,
,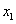 <
<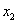 ,则
,则
所以 在区间
在区间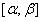 上是增函数,故
上是增函数,故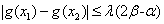 等价于
等价于
 (这可以由上面的
(这可以由上面的 化入韦达定理即可得
化入韦达定理即可得 )
)
又因为
所以 
 在
在 时奇函数且递增所以
时奇函数且递增所以
所以
 ,所以
,所以

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 满足
满足 ,则使不等式
,则使不等式 +
+ ≥
≥ 恒成立的实数
恒成立的实数 的取值范围是__________.
的取值范围是__________. sin2x+m-1=0在x∈(
sin2x+m-1=0在x∈( ,π)上有两个不同的实数根,则m的取值范围是________.
,π)上有两个不同的实数根,则m的取值范围是________. 的通项公式为
的通项公式为 ,数列
,数列 的通项公式为
的通项公式为 ,
, 若在数列
若在数列 中,
中, 对任意
对任意 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 为
为 的函数,对任意
的函数,对任意 ,
, ,且
,且 ,
, ,则集合A中的最小元素是______.
,则集合A中的最小元素是______.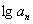 ,b3=18,b6=12,则数列{bn}前n项和的最大值等于
,b3=18,b6=12,则数列{bn}前n项和的最大值等于  ,当
,当 时,则方程
时,则方程 的根最多个数是
的根最多个数是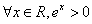 ”的否定是“
”的否定是“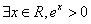 ”
”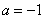 ,则函数
,则函数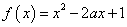 只有一个零点”的逆命题为真命题
只有一个零点”的逆命题为真命题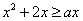 在
在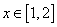 上恒成立”
上恒成立”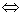 “
“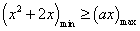 在
在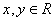 ,若
,若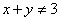 ,则
,则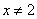 或
或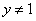 ”是真命题
”是真命题 ,4) (B)(-
,4) (B)(-