题目内容
1.打扑克的赵、钱、孙、李四家各从一副扑克的52张(去掉两张王牌后)中随机抽取13张,A=“赵家没得到2”,B=“孙家得到1张2”.(1)计算P(B|A);
(2)计算P(A|B);
(3)计算P(A∩B);
(4)计算P(A∪B).
分析 求出P(A),P(B),即可求得结论.
解答 解:P(A)=$\frac{{C}_{48}^{13}}{{C}_{52}^{13}}$,P(B)=$\frac{{C}_{4}^{1}{C}_{48}^{12}}{{C}_{52}^{13}}$,P(AB)=$\frac{{C}_{48}^{13}{C}_{4}^{1}{C}_{35}^{12}}{{C}_{52}^{13}{C}_{39}^{13}}$
(1)P(B|A)=$\frac{P(AB)}{P(A)}$=$\frac{{C}_{48}^{13}{C}_{4}^{1}{C}_{35}^{12}}{{C}_{52}^{13}{C}_{39}^{13}}$÷$\frac{{C}_{48}^{13}}{{C}_{52}^{13}}$=$\frac{{C}_{4}^{1}{C}_{35}^{12}}{{C}_{39}^{13}}$≈0.411;
(2)P(A|B)=$\frac{P(AB)}{P(B)}$=$\frac{{C}_{48}^{13}{C}_{4}^{1}{C}_{35}^{12}}{{C}_{52}^{13}{C}_{39}^{13}}$÷$\frac{{C}_{4}^{1}{C}_{48}^{12}}{{C}_{52}^{13}}$≈0.182;
(3)P(A∩B)=$\frac{{C}_{48}^{13}}{{C}_{52}^{13}}$•$\frac{{C}_{4}^{1}{C}_{48}^{12}}{{C}_{52}^{13}}$;
(4)P(A∪B)=$\frac{{C}_{48}^{13}}{{C}_{52}^{13}}$+$\frac{{C}_{4}^{1}{C}_{48}^{12}}{{C}_{52}^{13}}$.
点评 本题考查概率的计算,考查学生的计算能力,比较基础.

 阅读快车系列答案
阅读快车系列答案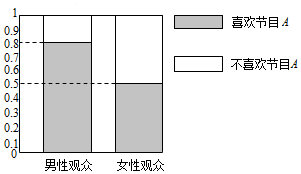 某媒体为调查喜欢娱乐节目A是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
某媒体为调查喜欢娱乐节目A是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:(Ⅰ)根据该等高条形图,完成下列2×2列联表,并独立性检验的方法分析,能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目A与观众性别有关?
| 喜欢节目A | 不喜欢节目A | 总计 | |
| 男性观众 | 24 | 6 | 30 |
| 女性观众 | 15 | 15 | 30 |
| 总计 | 39 | 21 | 60 |
附:
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |

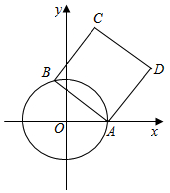 已知圆O为单位圆:x2+y2=1,点A(1,0),B为单位圆上的动点,如图,以AB为边作正方形ABCD,求动点D的轨迹方程及OD的取值范围.
已知圆O为单位圆:x2+y2=1,点A(1,0),B为单位圆上的动点,如图,以AB为边作正方形ABCD,求动点D的轨迹方程及OD的取值范围.