题目内容
5．若函数y=f（x）的定义域为R+，且f（xy）=f（x）+f（y），f（8）=3，则f（2$\sqrt{2}$）等于$\frac{3}{2}$．分析 根据抽象函数关系进行化简转化即可．
解答 解：∵f（xy）=f（x）+f（y），f（8）=3，
∴f（2$\sqrt{2}$）+f（2$\sqrt{2}$）=f（2$\sqrt{2}$×2$\sqrt{2}$）=f（8）=3，
则f（2$\sqrt{2}$）=$\frac{3}{2}$，
故答案为：$\frac{3}{2}$．
点评 本题主要考查函数值的求解，根据抽象函数关系进行转化求解即可．
练习册系列答案
相关题目
15．通过随机询问110名性别不同的大学生是否爱好体育，得到如表的列联表：
由公式算得：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}≈7.8$
附表：
参照附表，得到的正确结论是（ ）
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
附表：
| P（K2≥K0） | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A． | 有99%以上的把握认为“爱好体育运动与性别有关” | |
| B． | 有99%以上的把握认为“爱好体育运动与性别无关” | |
| C． | 在犯错误的概率不超过0.1%的前提下，认为“爱好体育运动与性别有关” | |
| D． | 在犯错误的概率不超过0.1%的前提下，认为“爱好体育运动与性别无关” |
16．
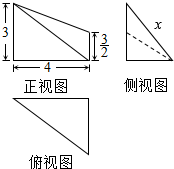某几何体的三视图如图所示，若该几何体的体积为3$\sqrt{7}$，则侧视图中线段的长度x的值是（ ）
某几何体的三视图如图所示，若该几何体的体积为3$\sqrt{7}$，则侧视图中线段的长度x的值是（ ）| A． | 5 | B． | 4 | C． | 2$\sqrt{7}$ | D． | $\sqrt{7}$ |
13．已知函数f（x）=（-x2+ax+b）（ex-e），当x＞0时，f（x）≤0，则实数a的取值范围为（ ）
| A． | a＞0 | B． | 0＜a≤1 | C． | a≥1 | D． | a≤1 |
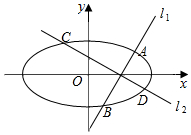在平面直角坐标系中，已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，F为椭圆的右焦点，过点F任作一条直线l1，交椭圆E于A，B两点，当l1垂直于x轴时，|AB|=1．