题目内容
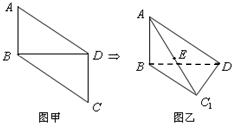 如图,在平行四边形ABCD中,AB=1,BD=
如图,在平行四边形ABCD中,AB=1,BD=| 2 |
(1)求证:平面ABD⊥平面BC1D;
(2)E为线段AC1上的一个动点,当线段EC1的长为多少时,DE与平面BC1D所成的角为30°?
分析:(1)利用勾股定理及其逆定理、线面垂直的判定定理、面面垂直的判定定理即可证明;
(2)通过建立空间直角坐标系,利用斜线的方向向量与平面的法向量所成的角即可得到线面角.
(2)通过建立空间直角坐标系,利用斜线的方向向量与平面的法向量所成的角即可得到线面角.
解答: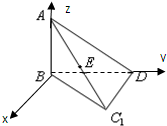 (1)证明:∵AB=1,BD=
(1)证明:∵AB=1,BD=
,∠ABD=90°,∴AD=
=
=BC,
∵AC1=2,∴AC12=AB2+BC12,∴∠ABC1=90°,∴AB⊥BC1.
又AB⊥BD,BC1∩BD=B,∴AB⊥平面BC1D,
∵AB?平面ABD,∴平面ABD⊥平面BC1D.
(2)在平面BC1D过点B作直线l⊥BD,分别以直线l,BD,BA为x,y,z建立空间直角坐标系B-xyz,
则A(0,0,1),C1(1,
,0),D(0,
,0),
∴
=(1,
,-1),
=(0,0,1),
设
=λ
=(λ,
λ,-λ),则E(λ,
λ,1-λ),λ∈[0,1],∴
=(λ,
λ-
,1-λ).
又
=(0,0,1)是平面BC1D的一个法向量,
依题意得sin30o=|cos<
,
>|,即|
|=
,
解得λ=
,即|C1E|=1时,DE与平面BC1D所成的角为30°.
 (1)证明:∵AB=1,BD=
(1)证明:∵AB=1,BD=| 2 |
12+(
|
| 3 |
∵AC1=2,∴AC12=AB2+BC12,∴∠ABC1=90°,∴AB⊥BC1.
又AB⊥BD,BC1∩BD=B,∴AB⊥平面BC1D,
∵AB?平面ABD,∴平面ABD⊥平面BC1D.
(2)在平面BC1D过点B作直线l⊥BD,分别以直线l,BD,BA为x,y,z建立空间直角坐标系B-xyz,
则A(0,0,1),C1(1,
| 2 |
| 2 |
∴
| AC1 |
| 2 |
| BA |
设
| AE |
| AC1 |
| 2 |
| 2 |
| DE |
| 2 |
| 2 |
又
| BA |
依题意得sin30o=|cos<
| BA |
| DE |
| 1-λ | ||
|
| 1 |
| 2 |
解得λ=
| 1 |
| 2 |
点评:熟练掌握勾股定理及其逆定理、线面垂直的判定定理、面面垂直的判定定理、通过建立空间直角坐标系并利用斜线的方向向量与平面的法向量所成的角求得到线面角是解题的关键.

练习册系列答案
相关题目
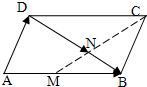
 如图,在平行四边形ABCD中,下列结论中错误的是( )
如图,在平行四边形ABCD中,下列结论中错误的是( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图,在平行四边形ABCD,
如图,在平行四边形ABCD, 如图,在平行四边形ABCD中,
如图,在平行四边形ABCD中,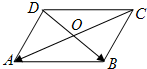 如图,在平行四边形ABCD中,若
如图,在平行四边形ABCD中,若 如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的中点.
如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的中点.