Question

【题目】已知命题：方程有两个不相等的实数根；命题：不等式的解集为.若或为真，为假，求实数的取值范围.

【答案】或

【解析】

根据“或为真，为假”判断出“为真，为假”，利用判别式列不等式分别求得为假、为真时的取值范围，再取两者的交集求得实数的取值范围.

因为或为真，为假，所以为真，为假

为假，，即：，∴或 ,

为真，，即：，∴或,

所以取交集为或 .

【点睛】

本小题主要考查含有简单逻辑联结词命题的真假性，考查一元二次方程根与判别式的关系，考查一元二次不等式解集为与判别式的关系，属于中档题.

【题型】解答题
【结束】
18

【题目】已知双曲线的中心在原点，焦点为，且离心率.

（1）求双曲线的方程；

（2）求以点为中点的弦所在的直线方程.

Answer 1

【答案】（1）；（2）.

【解析】

（1）根据焦点坐标求得,根据离心率及求得的值，进而求得双曲线的标准方程.（2）设出两点的坐标，利用点差法求得弦所在直线的斜率，再由点斜式求得弦所在的直线方程.

（1） 由题可得，，∴，,

所以双曲线方程 .

（2）设弦的两端点分别为，，

则由点差法有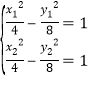： , 上下式相减有：

又因为为中点，所以，,

∴，所以由直线的点斜式可得,

即直线的方程为.

经检验满足题意.