题目内容
【题目】(本小题满分12分)
已知抛物线C的方程C:y2="2" p x(p>0)过点A(1,-2).
(I)求抛物线C的方程,并求其准线方程;
(II)是否存在平行于OA(O为坐标原点)的直线l,使得直线l与抛物线C有公共点,且直线OA与l的距离等于![]() ?若存在,求出直线l的方程;若不存在,说明理由。
?若存在,求出直线l的方程;若不存在,说明理由。
【答案】(I)抛物线C的方程为![]() ,其准线方程为
,其准线方程为![]() (II)符合题意的直线l 存在,其方程为2x+y-1 =0.
(II)符合题意的直线l 存在,其方程为2x+y-1 =0.
【解析】
试题(Ⅰ)求抛物线标准方程,一般利用待定系数法,只需一个独立条件确定p的值:(-2)2=2p·1,所以p=2.再由抛物线方程确定其准线方程:![]() ,(Ⅱ)由题意设
,(Ⅱ)由题意设![]() :
:![]() ,先由直线OA与
,先由直线OA与![]() 的距离等于
的距离等于![]() 根据两条平行线距离公式得:
根据两条平行线距离公式得:![]() 解得
解得![]() ,再根据直线
,再根据直线![]() 与抛物线C有公共点确定
与抛物线C有公共点确定![]()
试题解析:解 (1)将(1,-2)代入y2=2px,得(-2)2=2p·1,
所以p=2.
故所求的抛物线C的方程为![]()
其准线方程为![]() .
.
(2)假设存在符合题意的直线![]() ,
,
其方程为![]() .
.
由![]() 得
得![]() .
.
因为直线![]() 与抛物线C有公共点,
与抛物线C有公共点,
所以Δ=4+8t≥0,解得![]() .
.
另一方面,由直线OA到![]() 的距离
的距离![]()
可得![]() ,解得
,解得![]() .
.
因为-1[-![]() ,+∞),1∈[-
,+∞),1∈[-![]() ,+∞),
,+∞),
所以符合题意的直线![]() 存在,其方程为
存在,其方程为![]() .
.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
【题目】已知某校5个学生期末考试数学成绩和总分年级排名如下表:
学生的编号 | 1 | 2 | 3 | 4 | 5 |
数学 | 115 | 112 | 93 | 125 | 145 |
年级排名 | 250 | 300 | 450 | 70 | 10 |
(1)通过大量事实证明发现,一个学生的数学成绩和总分年级排名具有很强的线性相关关系,在上述表格是正确的前提下,用![]() 表示数学成绩,用
表示数学成绩,用![]() 表示年级排名,求
表示年级排名,求![]() 与
与![]() 的回归方程;(其中
的回归方程;(其中![]() 都取整数)
都取整数)
(2)若在本次考试中,预计数学分数为120分的学生年级排名大概是多少?
参考数据和公式:![]() ,其中
,其中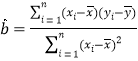 ,
,![]() ,其中
,其中![]()