题目内容
要得到f(x)=cos(2x+
)的图象，只需把y=sin2x的图象（ ）
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：将两个函数化为同名函数，结合三角函数的平移规律即可得到结论．
解答：
解：y=sin2x=cos（
-2x）=cos（2x-
），
∵f(x)=cos(2x+
)=cos[2（x+
）-
]的图象，
∴只需把y=sin2x的图象向左平移
个单位长度，即可，
故选：A．
| π |
| 2 |
| π |
| 2 |
∵f(x)=cos(2x+
| π |
| 3 |
| 5π |
| 12 |
| π |
| 2 |
∴只需把y=sin2x的图象向左平移
| 5π |
| 12 |
故选：A．
点评：本题主要考查三角函数图象之间的关系，利用了y=Asin（ωx+φ）的图象变换规律，统一这两个三角函数的名称，是解题的关键，属于基础题．
练习册系列答案
相关题目
已知实数a，b，c，d满足
=
=1，则（a-c）2+（b-d）2的最小值为（ ）
| lna |
| b |
| d2-2d |
| -c2 |
A、
| ||||
B、2-
| ||||
C、3-2
| ||||
D、1-
|
已知向量
=（x-4，1），
=（x+5，y），x，y∈（0，+∞），且
∥
，则xy取最小值时y的值为（ ）
| a |
| b |
| a |
| b |
| A、3 | ||
B、
| ||
| C、2 | ||
| D、1 |
以下事件：
（1）连续投掷骰子两次，掷得的点数和为16
（2）若集合A，B，C，满足A⊆B，B⊆C，则A⊆C
（3）骑车通过5个十字路口，一路绿灯
（4）技术发达后，不需要任何能量的永动机将会出现
（5）一教师在讲台上随手抛出一段粉笔头，粉笔头最后落下
属于随机事件的有（ ）
（1）连续投掷骰子两次，掷得的点数和为16
（2）若集合A，B，C，满足A⊆B，B⊆C，则A⊆C
（3）骑车通过5个十字路口，一路绿灯
（4）技术发达后，不需要任何能量的永动机将会出现
（5）一教师在讲台上随手抛出一段粉笔头，粉笔头最后落下
属于随机事件的有（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
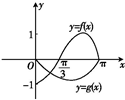已知y=f（x）是偶函数，y=g（x）是奇函数，它们的定义域均为[-π，π]，且它们在x∈[0，π]上的图象如图所示，则不等式| f(x) |
| g(x) |
A、（-
| ||||||
B、（
| ||||||
C、（-
| ||||||
D、（-
|