题目内容
给出定理,圆内接四边形的对角互补直线l1:x+3y-7=0、l2:kx-y-2=0与x轴、y轴的正半轴所围成的四边形有外接圆,则k为何值时l1:x+3y-7=0和l2:kx-y-2=0与x轴、y轴所围成的四边形有外接圆?并求此外接圆的标准方程.
考点:圆的标准方程
专题:直线与圆
分析:两直线与两坐标轴围成的四边形有外接圆,得到两直线垂直,即斜率的乘积为-1,求出k的值,求出圆的半径,写出圆的标准方程即可.
解答:
解:若两线x+3y-7=0 与kx-y-2=0于两坐标轴围成的四边形有外接圆,
∵坐标轴的夹角为90°,
∴两直线两线x+3y-7=0 与kx-y-2=0垂直,即-
k=-1,
解得:k=3,
即3x-y-2=0,此时直线与x轴的交点坐标为D(
,0),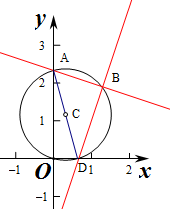
直线x+3y-7=0与y轴的交点坐标为A(0,
),
则A,B的中点坐标即外接圆的圆心坐标为C(
,
),
半径为
|AD|=
,
则此外接圆的方程为(x-
)2+(y-
)2=
.
∵坐标轴的夹角为90°,
∴两直线两线x+3y-7=0 与kx-y-2=0垂直,即-
| 1 |
| 3 |
解得:k=3,
即3x-y-2=0,此时直线与x轴的交点坐标为D(
| 2 |
| 3 |

直线x+3y-7=0与y轴的交点坐标为A(0,
| 7 |
| 3 |
则A,B的中点坐标即外接圆的圆心坐标为C(
| 1 |
| 3 |
| 7 |
| 6 |
半径为
| 1 |
| 2 |
| ||
| 6 |
则此外接圆的方程为(x-
| 1 |
| 3 |
| 7 |
| 6 |
| 53 |
| 36 |
点评:本题主要考查圆的标准方程,根据条件求出k,确定出圆心与半径是解本题的关键.

练习册系列答案
相关题目
已知三棱锥D-ABC的三个侧面与底面全等,且AB=AC=
,BC=2,则二面角A-BC-D的大小为( )
| 3 |
A、arccos
| ||||
B、arccos
| ||||
C、
| ||||
D、
|
某射手在一次射击中,射中10环、9环、8环的概率分别是0.20,0.30,0.20,则此射手在一次射击中不足8环的概率为( )
| A、0.40 | B、0.30 |
| C、0.60 | D、0.90 |
直线l1:x+(m+1)y+m-2=0与l2:mx+2y+8=0平行,则m的值为( )
| A、1 | B、-2 | C、2 | D、-2或1 |
函数y=2sin2x的图象可看成是由y=sinx的图象按下列哪种变换得到的?( )
A、横坐标不变,纵坐标变为原来的
| ||
B、纵坐标变为原来的2倍,横坐标变为原来的
| ||
| C、横坐标不变,纵坐标变为原来的2倍 | ||
D、纵坐标变为原来的
|