题目内容
12.若x,y∈R+,xy2=4,则x+2y的最小值,x+y的最小值.分析 根据条件便可得到$x=\frac{4}{{y}^{2}}$,从而根据三个数的均值不等式可以得到$x+2y=\frac{4}{{y}^{2}}+y+y≥3\root{3}{4}$,并可得出“=”成立的条件,这样便可求出x+2y的最小值,而同理可以求出x+y的最小值.
解答 解:∵x,y∈R+,xy2=4;
∴$x=\frac{4}{{y}^{2}}$;
∴$x+2y=\frac{4}{{y}^{2}}+y+y≥3\root{3}{\frac{4}{{y}^{2}}•y•y}=3\root{3}{4}$,当且仅当x=y=$\root{3}{4}$时取“=”;
∴x+2y的最小值为$3\root{3}{4}$;
同理,$x+y=\frac{4}{{y}^{2}}+\frac{y}{2}+\frac{y}{2}≥3\root{3}{\frac{4}{{y}^{2}}•\frac{y}{2}•\frac{y}{2}}=3$,当且仅当x=1,y=2时取“=”;
∴x+y的最小值为3.
点评 考查基本不等式用于求最值的方法,注意在应用$a+b+c≥3\root{3}{abc}$求a+b+c最小值时,应使得abc为常数,且a,b,c>0,并会判断“=”成立的条件.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
7.已知e是自然对数的底数,函数f(x)的定义域为R,2f(x)•2f′(x)>2,f(0)=8,则不等式$\frac{f(x)-1}{{e}^{ln7-x}}$>1的解集为( )
| A. | (-∞,0) | B. | (0,+∞) | C. | (1,+∞) | D. | (-∞,1) |
8.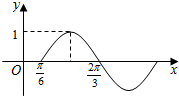 函数f(x)=sin(ωx+φ)(x∈R)$(ω>0,|φ|<\frac{π}{2})$的部分图象如图所示,如果${x_1},{x_2}∈(\frac{π}{6},\frac{2π}{3})$,且f(x1)=f(x2),则f(x1+x2)=( )
函数f(x)=sin(ωx+φ)(x∈R)$(ω>0,|φ|<\frac{π}{2})$的部分图象如图所示,如果${x_1},{x_2}∈(\frac{π}{6},\frac{2π}{3})$,且f(x1)=f(x2),则f(x1+x2)=( )
 函数f(x)=sin(ωx+φ)(x∈R)$(ω>0,|φ|<\frac{π}{2})$的部分图象如图所示,如果${x_1},{x_2}∈(\frac{π}{6},\frac{2π}{3})$,且f(x1)=f(x2),则f(x1+x2)=( )
函数f(x)=sin(ωx+φ)(x∈R)$(ω>0,|φ|<\frac{π}{2})$的部分图象如图所示,如果${x_1},{x_2}∈(\frac{π}{6},\frac{2π}{3})$,且f(x1)=f(x2),则f(x1+x2)=( )| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |