题目内容
8.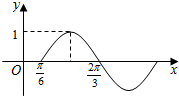 函数f(x)=sin(ωx+φ)(x∈R)$(ω>0,|φ|<\frac{π}{2})$的部分图象如图所示,如果${x_1},{x_2}∈(\frac{π}{6},\frac{2π}{3})$,且f(x1)=f(x2),则f(x1+x2)=( )
函数f(x)=sin(ωx+φ)(x∈R)$(ω>0,|φ|<\frac{π}{2})$的部分图象如图所示,如果${x_1},{x_2}∈(\frac{π}{6},\frac{2π}{3})$,且f(x1)=f(x2),则f(x1+x2)=( )| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 由周期求出ω,由五点法作图求出φ的值,可得函数的解析式,再根据正弦函数图象的对称性,求得 x1+x2=$\frac{5π}{6}$,可得f(x1+x2)的值.
解答 解:由函数f(x)=sin(ωx+φ)(x∈R)$(ω>0,|φ|<\frac{π}{2})$的部分图象,
可得$\frac{1}{2}$•$\frac{2π}{ω}$=$\frac{2π}{3}$-$\frac{π}{6}$,∴ω=2.
再根据五点法作图可的2•$\frac{π}{6}$+φ=0,∴φ=-$\frac{π}{3}$,f(x)=sin(2x-$\frac{π}{3}$).
在${x_1},{x_2}∈(\frac{π}{6},\frac{2π}{3})$上,且f(x1)=f(x2),则$\frac{1}{2}$(x1+x2)=$\frac{\frac{π}{6}+\frac{2π}{3}}{2}$,
∴x1+x2=$\frac{5π}{6}$,f(x1+x2)=sin(2•$\frac{5π}{6}$-$\frac{π}{3}$)=sin$\frac{4π}{3}$=-sin$\frac{π}{3}$=-$\frac{\sqrt{3}}{2}$,
故选:A.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由五点法作图求出φ的值,正弦函数的图象的对称性,属于基础题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
3.以椭圆$\frac{x^2}{4}+\frac{y^2}{2}$=1的焦距为实轴,短轴为虚轴的双曲线方程为( )
| A. | x2-4y2=2 | B. | x2-y2=2 | C. | x2-2y2=1 | D. | 2x2-y2=1 |
18.如图为某几何体的三视图,则该几何体的体积等于( )
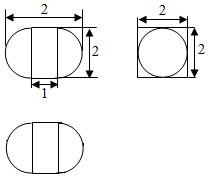

| A. | $4+\frac{2π}{3}$ | B. | $8+\frac{2π}{3}$ | C. | $4+\frac{4π}{3}$ | D. | $6+\frac{4π}{3}$ |