题目内容
已知函数f(x)=asinx+bx的图象在点(
,f(
))处的切线方程为x+2y-
+
=0.
(Ⅰ)求实数a,b的值;
(Ⅱ)当0<x<
时,f(x)>(m-1)x恒成立,求实数m的取值范围.
| π |
| 3 |
| π |
| 3 |
| 3 |
| π |
| 3 |
(Ⅰ)求实数a,b的值;
(Ⅱ)当0<x<
| π |
| 2 |
考点:导数在最大值、最小值问题中的应用
专题:综合题,导数的综合应用
分析:(Ⅰ)求导数f'(x)=acosx+b,由题意可得
,解出即可;
(Ⅱ)由(I)知f(x)=sinx-x,当0<x<
时,f(x)>(m-1)x恒成立等价于m<
恒成立,记g(x)=
,x∈(0,
),则问题进而化为m<g(x)min,利用导数可求得g(x)min;
|
(Ⅱ)由(I)知f(x)=sinx-x,当0<x<
| π |
| 2 |
| sinx |
| x |
| sinx |
| x |
| π |
| 2 |
解答:
解:(I)f'(x)=acosx+b,
由于直线x+2y-
+
=0的斜率为-
且过点(
,
-
),
∴
,
解得a=1,b=-1;
(Ⅱ)由(I)知f(x)=sinx-x,
当0<x<
时,f(x)>(m-1)x恒成立等价于m<
恒成立,
记g(x)=
,x∈(0,
),则g′(x)=
,
记h(x)=xcosx-sinx,则h'(x)=-xsinx<0,
∴h(x)在区间(0,
)上单调递减,h(x)<h(0)=0,
故g'(x)<0,∴g(x)在区间(0,
)上单调递减,g(x)>g(
)=
,
∴m≤
,
实数m的取值范围为(-∞,
].
由于直线x+2y-
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| ||
| 2 |
| π |
| 3 |
∴
|
解得a=1,b=-1;
(Ⅱ)由(I)知f(x)=sinx-x,
当0<x<
| π |
| 2 |
| sinx |
| x |
记g(x)=
| sinx |
| x |
| π |
| 2 |
| xcosx-sinx |
| x2 |
记h(x)=xcosx-sinx,则h'(x)=-xsinx<0,
∴h(x)在区间(0,
| π |
| 2 |
故g'(x)<0,∴g(x)在区间(0,
| π |
| 2 |
| π |
| 2 |
| 2 |
| π |
∴m≤
| 2 |
| π |
实数m的取值范围为(-∞,
| 2 |
| π |
点评:本题考查导数的几何意义、利用导数求函数的最值及函数恒成立问题,考查转化思想,考查学生分析解决问题的能力.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
 四棱锥P-ABCD的底面是边长为2的菱形,∠DAB=60°,侧棱PA=PC=2
四棱锥P-ABCD的底面是边长为2的菱形,∠DAB=60°,侧棱PA=PC=2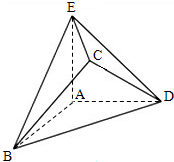 如图,在几何体ABCDE中,AB=AD=BC=DC=2,AE=2
如图,在几何体ABCDE中,AB=AD=BC=DC=2,AE=2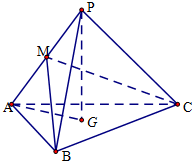 如图,三棱锥P-ABC中,AB=AC=2
如图,三棱锥P-ABC中,AB=AC=2