题目内容
设函数f(x)=lnx+
x-a(a∈R),若存在b∈[1,e],(e为自然对数的底数),使得f(f(b))=b,则实数a的取值范围是( )
| 1 |
| 2 |
A、[-
| ||||
B、[1-
| ||||
C、[-
| ||||
D、[-
|
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:利用反函数将问题进行转化,再将解方程问题转化为函数的图象交点问题.
解答:
解解:由f(f(b))=b,可得f(b)=f-1(b),
其中f-1(x)是函数f(x)的反函数
因此命题“存在b∈[1,e]使f(f(b))=b成立”,转化为
“存在b∈[1,e],使f(b)=f-1(b)”,
即y=f(x)的图象与函数y=f-1(x)的图象有交点,
且交点的横坐标b∈[1,e],
∵y=f(x)的图象与y=f-1(x)的图象关于直线y=x对称,
∴y=f(x)的图象与函数y=f-1(x)的图象的交点必定在直线y=x上,
由此可得,y=f(x)的图象与直线y=x有交点,且交点横坐标b∈[1,e],
令:lnx+
x-a=x,则方程在[1,e]上一定有解
∴a=lnx-
x,
设g(x)=lnx-
x
则g′(x)=
-
=
,
当g′(x)=0.解得x=2,
∴函数g(x)=在[1,2]为增函数,在[2,e]上为减函数,
∴g(x)≤g(2)=ln2-1,
g(1)=-
,g(e)=1-
e,
故实数a的取值范围是[-
,ln2-1]
故选:C
其中f-1(x)是函数f(x)的反函数
因此命题“存在b∈[1,e]使f(f(b))=b成立”,转化为
“存在b∈[1,e],使f(b)=f-1(b)”,
即y=f(x)的图象与函数y=f-1(x)的图象有交点,
且交点的横坐标b∈[1,e],
∵y=f(x)的图象与y=f-1(x)的图象关于直线y=x对称,
∴y=f(x)的图象与函数y=f-1(x)的图象的交点必定在直线y=x上,
由此可得,y=f(x)的图象与直线y=x有交点,且交点横坐标b∈[1,e],
令:lnx+
| 1 |
| 2 |
∴a=lnx-
| 1 |
| 2 |
设g(x)=lnx-
| 1 |
| 2 |
则g′(x)=
| 1 |
| x |
| 1 |
| 2 |
| 2-x |
| 2x |
当g′(x)=0.解得x=2,
∴函数g(x)=在[1,2]为增函数,在[2,e]上为减函数,
∴g(x)≤g(2)=ln2-1,
g(1)=-
| 1 |
| 2 |
| 1 |
| 2 |
故实数a的取值范围是[-
| 1 |
| 2 |
故选:C
点评:本题给出含有根号与指数式的基本初等函数,在存在b∈[1,e]使f(f(b))=b成立的情况下,求参数a的取值范围.着重考查了基本初等函数的图象与性质、函数的零点存在性定理和互为反函数的两个函数的图象特征等知识,属于中档题

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
若一条直线与一个平面成72°角,则这条直线与这个平面内经过斜足的直线所成角中最大角等于( )
| A、72° | B、90° |
| C、108° | D、180° |
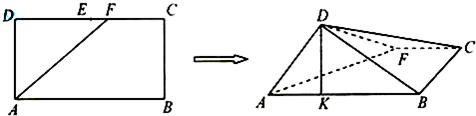
 如图,在空间四边形ABCD中,P、Q分别是△ABC和△BCD的重心,求证:PQ∥平面ACD.
如图,在空间四边形ABCD中,P、Q分别是△ABC和△BCD的重心,求证:PQ∥平面ACD.