题目内容
11. 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,离心率为$\frac{1}{2}$,过焦点F1的直线l交椭圆于A、B两点,且△ABF2的周长为8.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,离心率为$\frac{1}{2}$,过焦点F1的直线l交椭圆于A、B两点,且△ABF2的周长为8.(1)求椭圆C的方程;
(2)连接AO并延长交椭圆C于点Q,求△ABQ面积的最大值.并求此时直线l的方程.
分析 (1)根据椭圆定义及△ABF2的周长为8可知a=2,利用e=$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$=$\frac{1}{2}$计算可知b2=3,进而可得结论;
(2)通过(1)可故可设直线l的方程为x=ty-1,从而点O到直线l的距离d=$\frac{1}{\sqrt{1+{t}^{2}}}$,利用AO=OQ可知△ABQ面积的最大值即△ABO面积的最大值,通过联立直线l与椭圆C方程、利用韦达定理及两点间距离公式可知S△ABO=$\frac{1}{2}$•d•|AB|=$\frac{6\sqrt{1+{t}^{2}}}{4+3{t}^{2}}$,通过令m=$\sqrt{1+{t}^{2}}$换元、计算可知当m=1时S△ABO取最大值,进而可得结论.
解答 解:(1)根据椭圆定义及△ABF2的周长为8可知,
2a+2a=8,即a=2,
又∵e=$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$=$\frac{1}{2}$,即$\frac{\sqrt{4-{b}^{2}}}{2}$=$\frac{1}{2}$,
∴b2=3,
∴椭圆C的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)由(1)可知F1(-1,0),故可设直线l的方程为:x=ty-1,
则点O到直线l的距离d=$\frac{1}{\sqrt{1+{t}^{2}}}$,
∵S△ABO=S△BOQ,
∴△ABQ面积的最大值即△ABO面积的最大值,
联立直线l与椭圆C方程,消去x得:(4+3t2)y2-6ty-9=0,
设A(x1,y1),B(x2,y2),则
y1+y2=$\frac{6t}{4+3{t}^{2}}$,y1y2=-$\frac{9}{4+3{t}^{2}}$,
∴(y1-y2)2=(y1+y2)2-4y1y2=$\frac{144({t}^{2}+1)}{(4+3{t}^{2})^{2}}$,
∴|AB|2=(x1-x2)2+(y1-y2)2
=(1+t2)(y1-y2)2
=(1+t2)$\frac{144({t}^{2}+1)}{(4+3{t}^{2})^{2}}$
=$\frac{144(1+{t}^{2})^{2}}{(4+3{t}^{2})}$,
∴|AB|=$\frac{12(1+{t}^{2})}{4+3{t}^{2}}$,
∴S△ABO=$\frac{1}{2}$•d•|AB|
=$\frac{1}{2}$•$\frac{1}{\sqrt{1+{t}^{2}}}$•$\frac{12(1+{t}^{2})}{4+3{t}^{2}}$
=$\frac{6\sqrt{1+{t}^{2}}}{4+3{t}^{2}}$,
令m=$\sqrt{1+{t}^{2}}$∈[1,+∞),
则$\frac{12(1+{t}^{2})}{4+3{t}^{2}}$=$\frac{6m}{3{m}^{2}+1}$=$\frac{6}{3m+\frac{1}{m}}$,
∴当m=1时,S△ABO取最大值,
此时$\sqrt{1+{t}^{2}}$=1,即t=0,
∴直线l的方程为:x=-1.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,注意解题方法的积累,属于难题.

 步步高达标卷系列答案
步步高达标卷系列答案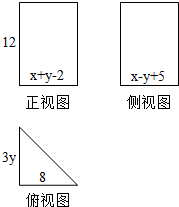 如图是一个几何体的三视图,请根据三视图的作图原则列出方程组,求出x,y的值及该几何体的表面积.
如图是一个几何体的三视图,请根据三视图的作图原则列出方程组,求出x,y的值及该几何体的表面积.