题目内容
在极坐标系中，曲线C1和C2的方程分别为ρsin2θ=2cosθ和ρsinθ=2，以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，则曲线C1和C2交点的直角坐标为 ．
考点：简单曲线的极坐标方程
专题：计算题,坐标系和参数方程
分析：运用x=ρcosθ，y=ρsinθ，即可化简曲线C1和C2的方程为普通方程，再联立解出交点即可．
解答：
解：曲线C1：ρsin2θ=2cosθ，即为ρ2sin2θ=2ρcosθ，
化为普通方程为：y2=2x，
曲线ρsinθ=2，化为普通方程为：y=2，
联立
解得
，
即交点的直角坐标为（2，2）．
故答案为：（2，2）．
化为普通方程为：y2=2x，
曲线ρsinθ=2，化为普通方程为：y=2，
联立
|
|
即交点的直角坐标为（2，2）．
故答案为：（2，2）．
点评：本题考查极坐标方程和普通方程的互化，考查解方程的运算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
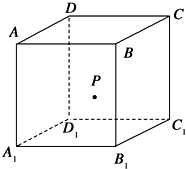如图正方体A1B1C1D1-ABCD的侧面AB1内有动点P到直线AB与到直线B1C1的距离相等，则动点P所在的曲线的形状为 （ ）
