题目内容
1．若（2x+$\sqrt{3}$）4=a0+a1x+a2x2+a3x3+a4x4，则（a0+a2+a4）2-（a1+a3）2的值为1．分析 通过对x赋值1和-1，求出各项系数和与正负号交替出现的系数和，两式相乘得解．
解答 解：（2x+$\sqrt{3}$）4=a0+a1x+a2x2+a3x3+a4x4中，
令x=1得${（2+\sqrt{3}）}^{4}$=a0+a1+a2+a3+a4，
令x=-1得${（-2+\sqrt{3}）}^{4}$=a0-a1+a2-a3+a4；
两式相乘得（3-4）4=（a0+a2+a4）2-（a1+a3）2=1．
故答案为：1．
点评 本题考查了利用赋值法求二项展开式系数和问题，是基础题．
练习册系列答案
相关题目
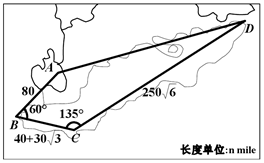某沿海四个城市A、B、C、D的位置如图所示，其中∠ABC=60°，∠BCD=135°，AB=80nmile，BC=40+30$\sqrt{3}$nmile，CD=250$\sqrt{6}$nmile，D位于A的北偏东75°方向．现在有一艘轮船从A出发以50nmile/h的速度向D直线航行，60min后，轮船由于天气原因收到指令改向城市C直线航行，收到指令时城市C对于轮船的方位角是南偏西θ度，则sinθ=$\frac{{\sqrt{6}-\sqrt{2}}}{4}$．
12．某单位共有10名员工，他们某年的收入如表：
（1）求该单位员工当年年薪的平均值和中位数；
（2）从该单位中任取2人，此2人中年薪收入高于7万的人数记为ξ，求ξ的分布列和期望；
（3）已知员工年薪收入与工作年限成正相关关系，某员工工作第一年至第四年的年薪分别为4万元，5.5万元，6万元，8.5万元，预测该员工第五年的年薪为多少？
附：线性回归方程$\widehaty=\widehatbx+\widehata$中系数计算公式分别为：$\widehatb=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}=\frac{7}{5}=1.4$，$\widehata=\overline y-\widehatb\overline x$，其中$\overline x，\overline y$为样本均值．
| 员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 年薪（万元） | 4 | 4.5 | 6 | 5 | 6.5 | 7.5 | 8 | 8.5 | 9 | 51 |
（2）从该单位中任取2人，此2人中年薪收入高于7万的人数记为ξ，求ξ的分布列和期望；
（3）已知员工年薪收入与工作年限成正相关关系，某员工工作第一年至第四年的年薪分别为4万元，5.5万元，6万元，8.5万元，预测该员工第五年的年薪为多少？
附：线性回归方程$\widehaty=\widehatbx+\widehata$中系数计算公式分别为：$\widehatb=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}=\frac{7}{5}=1.4$，$\widehata=\overline y-\widehatb\overline x$，其中$\overline x，\overline y$为样本均值．
9．已知函数f（x）=x2+bx+c在x=-1处取得极值-1，那么f（x）=（ ）
| A． | x2-2x-4 | B． | x2+x-1 | C． | x2+2x | D． | x2-2 |