题目内容
10.设Sn是数列{an}的前n项和,且a1=-2,Sn=2an+2,则an=-2n.分析 利用递推关系与等比数列的通项公式即可得出.
解答 解:∵Sn=2an+2,
∴当n≥2时,an=Sn-Sn-1=2an+2-(2an-1+2),
∴an=2an-1,
∴数列{an}是等比数列,公比为2,首项为-2.
∴an=-2×2n-1=-2n.
故答案为:-2n.
点评 本题考查了等比数列的通项公式、递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.设命题P:?x∈R,ex>1,则¬P为( )
| A. | ?x∈R,ex=1 | B. | ?x∈R,ex>1 | C. | ?x∈R,ex≤1 | D. | ?x∈R,ex≤1 |
2.对抛物线y=4x2,下列描述正确的是( )
| A. | 开口向右,焦点为(1,0) | B. | 开口向上,焦点为(0,1) | ||
| C. | 开口向上,焦点为(0,$\frac{1}{16}$) | D. | 开口向右,焦点为($\frac{1}{16}$,0) |
19.关于直线2x-y=2与直线x+2y=1的关系,正确的说法是( )
| A. | 重合 | B. | 相交但不垂直 | C. | 垂直 | D. | 平行 |
20.一梯形的直观图是一个如图所示的等腰梯形,且此梯形的面积为$\sqrt{2}$,则原梯形的面积为( )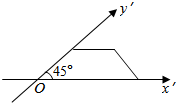

| A. | 2 | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 4 |