题目内容
两球的体积之比为:27:64,那么这两个球的表面积之比为 .
考点:球的体积和表面积
专题:空间位置关系与距离
分析:设两球的半径分别为r,R,由题意体积比可得r:R=3:4,进而可得表面积之比.
解答:
解:设两球的半径分别为r,R,
由题意可得
πr3:
πR3=27:64,
解得r:R=3:4,
∴两个球的表面积之比4πr2:4πR2=9:16
故答案为:9:16
由题意可得
| 4 |
| 3 |
| 4 |
| 3 |
解得r:R=3:4,
∴两个球的表面积之比4πr2:4πR2=9:16
故答案为:9:16
点评:本题考查球的表面积和体积公式,属基础题.

练习册系列答案
相关题目
 设抛物线y2=4x的焦点为F,过点(
设抛物线y2=4x的焦点为F,过点(| 1 |
| 2 |
(Ⅰ)求点M的轨迹方程;
(Ⅱ)设直线PQ的斜率为k,用k表示△APQ的面积.
已知α∈(
,π),且sinα•cosα=-
,则sinα-cosα的值是( )
| 3π |
| 4 |
| ||
| 4 |
A、±
| ||||
B、
| ||||
C、-
| ||||
D、
|
 如图,空间四边形ABCD中,P、Q、R分别是AB、AD、CD的中点,平面PQR交BC于点S.
如图,空间四边形ABCD中,P、Q、R分别是AB、AD、CD的中点,平面PQR交BC于点S.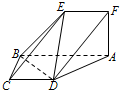 设平面ABCD⊥平面ABEF,AB∥CD,AB∥EF,∠BAF=∠ABC=90°,BC=CD=AF=EF=1,AB=2.
设平面ABCD⊥平面ABEF,AB∥CD,AB∥EF,∠BAF=∠ABC=90°,BC=CD=AF=EF=1,AB=2.