题目内容
2.已知函数f(x)=$\frac{x}{1+x}$.(1)作出函数f(x)的大致图象;
(2)指出函数f(x)的单调区间,并结合图象,指出不等式f(x)<2的解集.
分析 (1)由反比例函数及图象变换作函数f(x)的图象,
(2)结合图象可知f(x)在(-∞,-1),(-1,+∞)上是增函数,且f(-2)=2,从而解得.
解答 解:(1)作函数f(x)的图象如下,
(2)结合图象可知,
f(x)在(-∞,-1),(-1,+∞)上是增函数,
且f(-2)=2,
故结合图象可知,f(x)<2的解集为(-∞,-2)∪(-1,+∞).
点评 本题考查了反比例函数的图象的作法及图象的变换的应用,同时考查了函数与方程的关系应用及数形结合的思想,属于中档题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
17.圆(x+2)2+(y+2)2=4与圆(x-2)2+(y-1)2=9的公切线条数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
7.已知命题p:?x∈R,ex>1;命题q:?x0∈R,x0-2>log2x0,则下列命题中为真命题的是( )
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
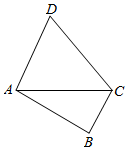 如图所示,在四边形ABCD中,已知AC=$\sqrt{6}+\sqrt{2}$,AD=2$\sqrt{2}$,DC=2$\sqrt{3}$,AD∥BC.
如图所示,在四边形ABCD中,已知AC=$\sqrt{6}+\sqrt{2}$,AD=2$\sqrt{2}$,DC=2$\sqrt{3}$,AD∥BC.