题目内容
【题目】如图,欲在一四边形花坛![]() 内挖一个等腰三角形的水池
内挖一个等腰三角形的水池![]() ,且
,且![]() ,已知四边形
,已知四边形![]() 中,
中,![]() 是等腰直角三角形,
是等腰直角三角形,![]() 米,
米,![]() 是等腰三角形,
是等腰三角形,![]() ,
,![]() 的大小为
的大小为![]() ,要求
,要求![]() 的三个顶点在花坛的边缘上(即在四边形
的三个顶点在花坛的边缘上(即在四边形![]() 的边上),设点
的边上),设点![]() 到水池底边
到水池底边![]() 的距离为
的距离为![]() ,水池的面积为
,水池的面积为![]() 平方米.
平方米.
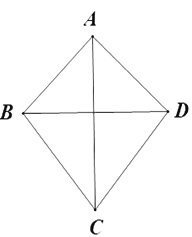
(1)求![]() 的长;
的长;
(2)试将![]() 表示成关于
表示成关于![]() 的函数,并求出
的函数,并求出![]() 的最大值.
的最大值.
【答案】(1)14;(2)![]() ,最大值为
,最大值为![]() ;
;
【解析】
(1) 设![]() 与
与![]() 交于
交于![]() ,在两个三角形中计算出
,在两个三角形中计算出![]() ,再相加即可得到;
,再相加即可得到;
(2)分![]() 和
和![]() 两种情况讨论得到
两种情况讨论得到![]() 关于
关于![]() 的函数,再分段求最大值,即可得到.
的函数,再分段求最大值,即可得到.
(1)设![]() 与
与![]() 交于
交于![]() ,如图所示:
,如图所示:

因为![]() ,
,![]() ,所以
,所以![]() 为
为![]() 的垂直平分线,所以
的垂直平分线,所以![]() 为
为![]() 的中点,
的中点,
所以![]() ,
,
在直角三角形![]() 中,
中,![]() ,
,
因为 ,
,
所以![]()
 ,
,
所以![]()
 ,
,
所以![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
所以 ,
,
所以![]() .
.
(2)因为![]() ,所以
,所以![]() 时
时![]() 的垂直平分线,,
的垂直平分线,,
所以当![]() 时,点
时,点![]() 在
在![]() 边上,所以
边上,所以![]() ,
,
所以![]() ,此时当
,此时当![]() 时,
时,![]() 取得最大值36,
取得最大值36,
当![]() 时,点
时,点![]() 在
在![]() 边上,此时
边上,此时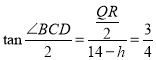 ,
,
所以![]() ,
,
所以![]()
![]() ,
,
所以当 ![]() 时,
时,![]() 取得最大值,最大值为
取得最大值,最大值为![]() .
.
因为![]() ,
,
所以当![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.
综上所述: ,
,![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目