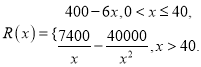题目内容
【题目】已知![]() ,
,![]() .
.
(1)若直线![]() 与圆
与圆![]() :
:![]() 相切,求
相切,求![]() 被圆
被圆![]() :
:![]() 所截得弦长取最小值时直线
所截得弦长取最小值时直线![]() 的斜率;
的斜率;
(2)![]() 时,
时,![]() :
:![]() 表示圆,问是否存在一条直线
表示圆,问是否存在一条直线![]() ,使得它和所有的圆
,使得它和所有的圆![]() 都没有公共点?如果存在,求出直线
都没有公共点?如果存在,求出直线![]() ,若不存在,说明理由;
,若不存在,说明理由;
(3)若满足不等式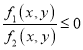 和等式
和等式![]() 的点集是一条线段,求
的点集是一条线段,求![]() 取值范围.
取值范围.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() :
:![]() ;(3)
;(3)![]() .
.
【解析】
(1)画出图像分析可得, 直线![]() 与直线
与直线![]() 垂直时
垂直时![]() 被圆
被圆![]() :
:![]() 所截得弦长取最小值.
所截得弦长取最小值.
再根据垂直的直线斜率之积为-1求解即可.
(2)当![]() 时代入
时代入![]() 有
有
![]() ,即
,即![]() 又
又![]() ,故猜测存在一条直线
,故猜测存在一条直线![]() ,使得它和所有的圆
,使得它和所有的圆![]() 都没有公共点,再证明即可.
都没有公共点,再证明即可.
(3) ![]() 的解集为
的解集为![]() 或
或![]() 两条直线,
两条直线, 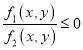 为两圆之间的部分,数形结合列式求解即可.
为两圆之间的部分,数形结合列式求解即可.
(1)由![]() ,
,
即![]() 圆心
圆心![]() ,半径
,半径![]()
![]()
即![]() 圆心
圆心![]() ,半径
,半径![]()
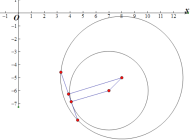
因为当![]() 被圆
被圆![]() :
:![]() 所截得弦长取最小值时,圆心
所截得弦长取最小值时,圆心![]() 到直线
到直线![]() 的距离最大.
的距离最大.
又![]() 到
到![]() 的距离
的距离![]() ,当且仅当直线
,当且仅当直线![]() 与直线
与直线![]() 垂直时取得
垂直时取得![]() 为最大值,此时
为最大值,此时![]() 斜率
斜率![]() ,故直线
,故直线![]() 斜率
斜率![]()
(2) 存在,![]() :
:![]() 和所有的圆
和所有的圆![]() 都没有公共点.
都没有公共点.
证明:由题![]() :
:![]() ,
,![]() 即
即
![]() ,
,
变形得![]()
即![]() ,
,
故![]() :
:![]()
若![]() 与
与![]() 有交点,则
有交点,则
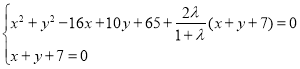 有解.上式减去
有解.上式减去![]() 倍的下式有:
倍的下式有:
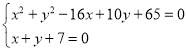 有解.
有解.
即圆![]() 与直线
与直线![]() 有交点,圆半径
有交点,圆半径![]()
但圆心![]() 到
到![]() 距离
距离![]() .
.
故圆![]() 与直线
与直线![]() 无交点.
无交点.
即![]() 和所有的圆
和所有的圆![]() 都没有公共点.
都没有公共点.
(3)由题得![]() 的解集为
的解集为![]() 或
或![]() 两条直线,
两条直线,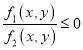 得
得![]() 且
且![]()
即为两圆![]()
![]() 与
与![]()
![]() 之间的部分.
之间的部分.
又若不等式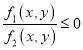 和等式
和等式![]() 的点集是一条线段,则需注意临界条件.
的点集是一条线段,则需注意临界条件.
当![]() 与圆
与圆![]() 相切时,
相切时,![]() 或
或![]() ,
,
当![]() 与圆
与圆![]() 相切时,
相切时,![]() 或
或![]()
又因为![]() 到所求的所有
到所求的所有![]() 的距离都大于半径
的距离都大于半径![]() ,故无需考虑圆
,故无需考虑圆![]() 对形成线段的影响.
对形成线段的影响.
故![]()

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目