题目内容
【题目】在长方体
，中，
，过
三点的平面D截去长方体的一个角后，得到如图所示的几何体
.
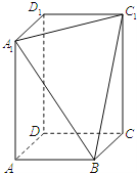
（1）求几何体的体积；
（2）求直线
与面
所成角.（用反三角表示）
【答案】（1）
;（2）
.
【解析】
（1）由已知中，图示的几何体
是由过
、
、
三点的平面截去长方体
得到，故
，将
,
代入即可得到答案；
（2）解以
为坐标原点建立空间直角坐标系，求出各点坐标，进而求出直线
的方向向量及平面
的法向量，代入直线与平面夹角的向量法公式，即可求出答案．
(1)
；
（2）以为坐标原点，分别以
,
,
所在直线为
轴，
轴，
轴建立空间直角坐标系，如图所示：
由题意可知：
，
，
，
，
,
,
，
设面的法向量是
,则
，取
得
，
设
与
的夹角为
，
则
，
设直线与面所成的角为
，
则
，
得直线与面 所成的角为.
练习册系列答案
相关题目
