题目内容
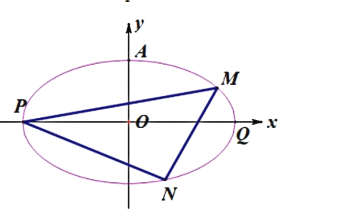
【题目】如图,已知椭圆![]() 的左、右两个焦点分别为
的左、右两个焦点分别为![]() 设
设![]() ,若
,若![]() 为正三角形且周长为
为正三角形且周长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过点![]() 且斜率为
且斜率为![]() 的直线与椭圆
的直线与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,是否存在实数
,是否存在实数![]() 使
使![]() 成立,若存在,求出
成立,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)若过点![]() 的直线与椭圆
的直线与椭圆![]() 相交于不同的两点
相交于不同的两点![]() 两点,
两点,![]() 记的面积记为
记的面积记为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】![]()
![]() ;
;![]() 答案见解析
答案见解析![]()
![]()
【解析】
(1)![]() 为正三角形且周长为
为正三角形且周长为![]() ,
,![]() 得周长等于
得周长等于![]() ,在
,在![]() 中
中![]() 故得
故得![]() ,在椭圆中有
,在椭圆中有![]() ,列出方程组即可求得
,列出方程组即可求得![]() 和
和![]() 的值进而求得椭圆方程;
的值进而求得椭圆方程;
(2)假设存在实数![]() 使
使![]() 成立,则
成立,则![]() .联立
.联立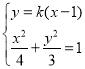 ,通过韦达定理求解
,通过韦达定理求解![]() ,若
,若![]() 有解,假设成立,否则不成立.
有解,假设成立,否则不成立.
(3)分类讨论,设直线![]() 的方程,代入椭圆方程,利用韦达定理及基本不等式的性质,即可求得
的方程,代入椭圆方程,利用韦达定理及基本不等式的性质,即可求得![]() 的取值范围.
的取值范围.
(1)![]()
![]() 为正三角形且周长为
为正三角形且周长为![]() ,故得:
,故得: ![]()
![]() 在
在![]() 中
中![]() ,故得
,故得![]()
![]() 椭圆
椭圆![]() , 故得
, 故得![]()
联立方程可得: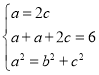
解得:![]()
故椭圆![]() 的标准方程:
的标准方程: ![]() .
.
(2)假设存在实数![]() 使
使![]() 成立,则
成立,则![]()
设点设![]() ,
,
则:![]()
![]() ①
①
设直线方程为![]()
联立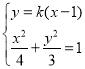 ,消掉y得
,消掉y得![]() ,
,
显然![]() ,方程有根,且
,方程有根,且![]()
![]() ②,
②, ![]()
![]() ③
③
将![]() 代入①式得:
代入①式得:![]()
![]() ④
④
把②③式代入④式得:![]()
化简可得:![]() 即:
即:![]() 得
得 ![]()
所以不存在实数![]() 使
使![]() 成立.
成立.
(3)当直线![]() 无斜率时,直线方程为
无斜率时,直线方程为![]() 此时
此时 ![]() ,
,![]() 记的面积记为
记的面积记为![]() ,
,![]()
当直线![]() 斜率存在(显然
斜率存在(显然![]() )时,设直线方程为
)时,设直线方程为![]()
设![]() ,联立
,联立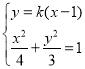 ,消掉y得
,消掉y得![]() ,
,
显然![]() 方程有根,且
方程有根,且![]() ,
, ![]()
此时![]()
因为![]() 则|
则|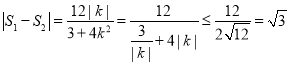 (
(![]() 时等号成立)
时等号成立)
所以![]() 的最大值为
的最大值为![]() ,则
,则![]()
![]()
![]() 的取值范围
的取值范围![]() .
.

练习册系列答案
相关题目