题目内容
【题目】如图，已知四棱锥S－ABCD的底面ABCD是正方形，SA⊥底面ABCD，E是SC上的一点.
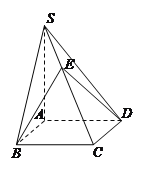
(1)求证：平面EBD⊥平面SAC；
(2)设SA＝4，AB＝2，求点A到平面SBD的距离；
【答案】(1)见解析（2）0.5
·
【解析】
(1)证明：∵SA⊥底面ABCD，BD底面ABCD，∴SA⊥BD
∵ABCD是正方形，∴AC⊥BD
∴BD⊥平面SAC，又BD平面EBD
∴平面EBD⊥平面SAC.
(2)解：设AC∩BD＝O，连结SO，则SO⊥BD
由AB＝2，知BD＝
SO＝
∴S△SBD＝
BD·SO＝··＝6
令点A到平面SBD的距离为h，由SA⊥平面ABCD, 则·S△SBD·h＝·S△ABD·SA
∴6h＝·2·2·4 h＝∴点A到平面SBD的距离为
练习册系列答案
相关题目
