题目内容

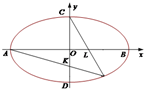如图，设椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）长轴为AB，短轴为CD，E是椭圆弧BD上的一点，AE交CD于K，CE交AB于L，则（
EK
AK
）2+（
EL
CL
）2的值为
 
．
考点：椭圆的简单性质
专题：转化思想,圆锥曲线的定义、性质与方程
分析：利用投影将斜距离之比转化为水平的距离或竖直的距离之比，将线段之比转化为坐标的绝对值之比，即可求出答案．
解答： 解：如图所示，设点E（x0，y0），过点E分别向x、y轴引垂线，垂足分别为N、M，
由△MKE∽△OKA，故
EK
AK
=
ME
AO
=
|x0|
a
，
同理
EL
CL
=
|y0|
b
，
则(
EK
AK
)2+(
EL
CL
)2=
x
2
0
a2
+
y
2
0
b2
，
又点E（x0，y0）在椭圆上，
∴
x
2
0
a2
+
y
2
0
b2
=1，
即(
EK
AK
)2+(
EL
CL
)2=1．
故答案为：1．
点评：本题考查了椭圆的几何性质的应用问题，解题时应利用转化思想，适当地转化所求的结果，体现了坐标法解决问题的优势，是中档题．
练习册系列答案
相关题目
（1）计算：C
 
2013
2014
+A
 
3
5
；
（2）观察下面一组组合数等式：C
 
1
n
=nC
 
0
n-1
；2C
 
2
n
=nC
 
1
n-1
；3C
 
3
n
=nC
 
2
n-1
；…由以上规律，请写出第k（k∈N*）个等式并证明．
已知f（x）=（x-1）lnx，g（x）=x3+（a-1）x2-ax．
（1）求函数f（x）在[t，t+
1
2
]（t＞0）上的最小值；
（2）是否存在整数a，使得对任意x∈[1，+∞），（x+1）f（x）≤g（x）恒成立，若存在，求a的最小值，若不存在，请说明理由．
若复数（m2-5m+6）+（m2-3m）i（m为实数，i为虚数单位）是纯虚数，则m=
 
．
将三个半径为3的球两两相切地放在水平桌面上，若在这三个球的上方放置一个半径为1的小球，使得这四个球两两相切，则该小球的球心到桌面的距离为
 
．
定义在区间[a，b]上的函数y=f（x），f′（x）是函数f（x）的导数，如果?ξ∈[a，b]，使得f（b）-f（a）=f′（ξ）（b-a），则称ξ为[a，b]上的“中值点”．下列函数：①f（x）=2x+1，②f（x）=x2-x+1，③f（x）=ln（x+1），④f（x）=（x-
1
2
）3．其中在区间[0，1]上的“中值点”多于一个的函数是
 
（请写出你认为正确的所有结论的序号）
已知函数f（x）是定义在R上的可导函数，其导函数记为f′（x），若对于任意的实数x，有f（x）＞f′（x），且y=f（x）-1是奇函数，则不等式f（x）＜ex的解集为
 
．
下列命题：
①?x∈R，使f（x）=（m-1）x m2-4m+3 是幂函数；且在（0，+∞）上递减；
②若0＜loga2＜logb2，则a＞b＞1；
③已知a，b∈R*，2a+b=1，则
2
a
+
1
b
有最小值8；
④已知向量
a
=（1，2），
b
=（2，0），若向量λ
a
+
b
与向量
c
=（1，-2）垂直，则实数λ等于-1．
其中，正确命题的序号为
 
．
随机变量ξ的取值为0，1，2，若P（ξ=0）=
1
5
，E（ξ）=1，则D（ξ）=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网