题目内容
已知双曲线 经过点
经过点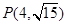 ,且双曲线
,且双曲线 的渐近线与圆
的渐近线与圆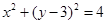 相切.
相切.
(1)求双曲线 的方程;
的方程;
(2)设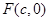 是双曲线
是双曲线 的右焦点,
的右焦点,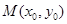 是双曲线
是双曲线 的右支上的任意一点,试判断以
的右支上的任意一点,试判断以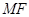 为直径的圆与以双曲线实轴为直径的圆的位置关系,并说明理由.
为直径的圆与以双曲线实轴为直径的圆的位置关系,并说明理由.
 经过点
经过点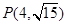 ,且双曲线
,且双曲线 的渐近线与圆
的渐近线与圆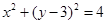 相切.
相切.(1)求双曲线
 的方程;
的方程;(2)设
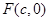 是双曲线
是双曲线 的右焦点,
的右焦点,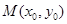 是双曲线
是双曲线 的右支上的任意一点,试判断以
的右支上的任意一点,试判断以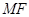 为直径的圆与以双曲线实轴为直径的圆的位置关系,并说明理由.
为直径的圆与以双曲线实轴为直径的圆的位置关系,并说明理由.(1)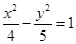 ;(2)外切.
;(2)外切.
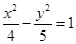 ;(2)外切.
;(2)外切.试题分析:(1)利用“点
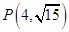 在双曲线
在双曲线 上”以及“双曲线
上”以及“双曲线 的渐近线与圆
的渐近线与圆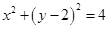 ”这两个条件列两个方程,求解
”这两个条件列两个方程,求解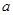 与
与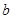 ,进而确定双曲线
,进而确定双曲线 的方程;(2)根据圆与圆的位置关系的判断方法,考查两圆连心线的长度与两圆半径之间的相互关系,同时注意将点
的方程;(2)根据圆与圆的位置关系的判断方法,考查两圆连心线的长度与两圆半径之间的相互关系,同时注意将点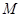 与左焦点
与左焦点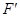 连接起来,注意到两圆圆心分别为
连接起来,注意到两圆圆心分别为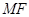 与
与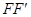 的中点,利用中位线以及双曲线的定义确定两圆半径与连心线长度之间的关系,进而确定两圆的位置关系.
的中点,利用中位线以及双曲线的定义确定两圆半径与连心线长度之间的关系,进而确定两圆的位置关系.试题解析:(1)因为双曲线
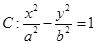 经过点
经过点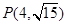 ,所以
,所以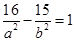 ①.
①.因为双曲线
 的的渐近线
的的渐近线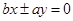 与圆
与圆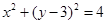 相切,
相切,所以圆心
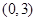 到直线
到直线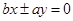 的距离等于2,
的距离等于2,即
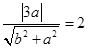 ,整理得
,整理得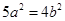 ②.
②.联立①与②,解得
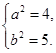 所以双曲线
所以双曲线 的方程为
的方程为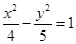 .
.(2)由(1)得,
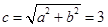 ,所以双曲线
,所以双曲线 的右焦点为
的右焦点为 .
.设双曲线
 的左焦点为
的左焦点为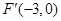 ,因为点
,因为点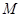 在双曲线
在双曲线 的右支上,
的右支上,所以
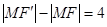 ,即
,即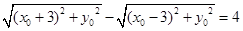 ,
,所以
 .
.因为以双曲线
 的实轴为直径的圆的圆心为
的实轴为直径的圆的圆心为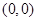 ,半径为
,半径为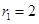 ;
;以
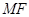 为直径的圆的圆心为
为直径的圆的圆心为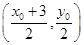 ,半径为
,半径为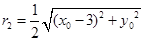 ,
,所以两圆圆心之间的距离为
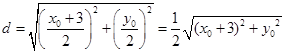 .
.因为
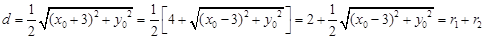 ,
,所以以
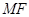 为直径的圆与以双曲线实轴为直径的圆外切.
为直径的圆与以双曲线实轴为直径的圆外切.
练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
 ,离心率为
,离心率为 ,且过点
,且过点 ,则曲线
,则曲线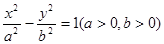 的右焦点为
的右焦点为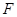 ,过
,过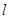 交双曲线的渐近线于
交双曲线的渐近线于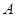 ,
, 两点,且与其中一条渐近线垂直,若
两点,且与其中一条渐近线垂直,若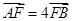 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )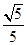
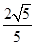
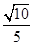
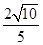
 轴上的双曲线
轴上的双曲线 的离心率为
的离心率为 ,则该双曲线的渐近线方程为( )
,则该双曲线的渐近线方程为( )



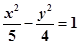 的顶点和焦点到其渐近线距离的比是( )
的顶点和焦点到其渐近线距离的比是( )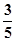
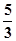
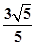
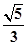
 的渐近线与圆
的渐近线与圆 有交点,则该双曲线的离心率的取值范围是___________.
有交点,则该双曲线的离心率的取值范围是___________. 的离心率为
的离心率为
 是右焦点.若
是右焦点.若 为双曲线上关于原点对称的两点,且
为双曲线上关于原点对称的两点,且 ,则直线
,则直线 的斜率是( )
的斜率是( )



 分别是双曲线
分别是双曲线 的左右焦点,
的左右焦点, 为双曲线的右顶点,线段
为双曲线的右顶点,线段 的垂直平分线交双曲线于
的垂直平分线交双曲线于 ,且
,且 ,则双曲线的离心率为
,则双曲线的离心率为



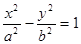 的渐近线方程是
的渐近线方程是 ,那么此双曲线的离心率为 .
,那么此双曲线的离心率为 .