题目内容
已知点 D 为ΔABC 的边 BC 上一点.且 BD ="2DC," 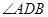 =750,
=750,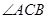 ="30°,AD" =
="30°,AD" =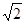 .
.
(I)求CD的长;
(II)求ΔABC的面积
(I)  ;(II)
;(II) .
.
解析试题分析:(I)由已知可得 ,在△ADC中已知两角及一边,应用正弦定理即可求解;(II)由(I)可知
,在△ADC中已知两角及一边,应用正弦定理即可求解;(II)由(I)可知 ,又
,又 ,
, ,要求ΔABC的面积,只需求出AC边的长即可.而AC边的长可通过解△ADC来实现.
,要求ΔABC的面积,只需求出AC边的长即可.而AC边的长可通过解△ADC来实现.
试题解析:
(I)因为 ,所以
,所以
在 中,
中, ,
,
根据正弦定理有 4分
4分
所以 ; 6分
; 6分
(II)所以 7分
7分
又在 中,
中, ,
, 9分
9分
所以 12分
12分
所以 13分
13分
同理,根据根据正弦定理有
而  8分
8分
所以 10分
10分
又 ,
, 11分
11分
所以 . 13分
. 13分
考点:正弦定理.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
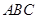 中,内角
中,内角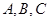 所对的边分别为
所对的边分别为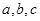 ,已知m
,已知m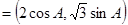 ,n
,n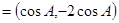 ,m·n
,m·n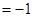 .
. 的大小;
的大小;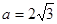 ,
, ,求△
,求△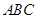 的三边为
的三边为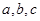 满足
满足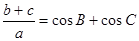 .
.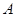 的值;
的值; 的取值范围.
的取值范围. ,
,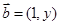 ,已知
,已知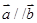 ,且有函数
,且有函数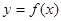 .
.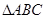 的三个内角分别为
的三个内角分别为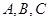 ,若有
,若有 ,边
,边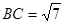 ,
,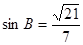 ,求
,求 的长及
的长及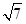 ,△ABC的面积为2
,△ABC的面积为2 ,求b+c.
,求b+c.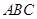 中,
中,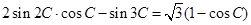 .
.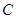 的大小;
的大小; ,且
,且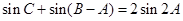 ,求
,求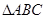 的面积.
的面积. 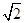 ,c=
,c= +1,求A
+1,求A ,∠ABC=
,∠ABC= .
.
 ;
; DC,求
DC,求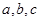 分别是角A,B,C的对边,
分别是角A,B,C的对边,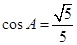 ,
,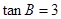 .
.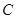 的值;
的值; ,求△ABC面积.
,求△ABC面积.