题目内容
设△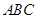 的三边为
的三边为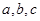 满足
满足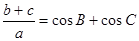 .
.
(Ⅰ)求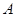 的值;
的值;
(Ⅱ)求 的取值范围.
的取值范围.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(Ⅰ)由 ,即含有角又含有边,像这一类题,可以利用正弦定理把边化成角,也可利用余弦定理把角化成边,本题两种方法都行,若利用正弦定理把边化成角,利用三角恒等变化,求出
,即含有角又含有边,像这一类题,可以利用正弦定理把边化成角,也可利用余弦定理把角化成边,本题两种方法都行,若利用正弦定理把边化成角,利用三角恒等变化,求出 角,若利用余弦定理把角化成边,利用代数恒等变化,找出边之间的关系,从而求出角
角,若利用余弦定理把角化成边,利用代数恒等变化,找出边之间的关系,从而求出角 ;(Ⅱ)求
;(Ⅱ)求 的取值范围,首先利用降幂公式,与和角公式,利用
的取值范围,首先利用降幂公式,与和角公式,利用 互余,将它化为一个角的一个三角函数,从而求出范围.
互余,将它化为一个角的一个三角函数,从而求出范围.
试题解析:(Ⅰ) ,所以
,所以 ,所以
,所以 ,所以
,所以 所以
所以 ,即
,即 ,所以
,所以 ,所以
,所以
(Ⅱ) =
= =
= 其中
其中 因为
因为 , 所以
, 所以 所以
所以
考点:正余弦定理的运用,三角恒等变化,求三角函数值域,考查学生的运算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,求C.
,求C. 中,角
中,角 所对的边分别为
所对的边分别为 ,设
,设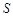 为
为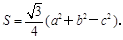
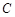 的大小;
的大小;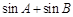 的最大值.
的最大值.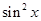 -sin(2x-
-sin(2x-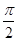 ).
).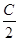 )=
)=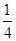 ,若sinB=2sinA,求△ABC的面积.
,若sinB=2sinA,求△ABC的面积. 中角
中角 的对边分别为
的对边分别为 ,且
,且 ,
, 的大小;
的大小; ,求
,求 的最大值。
的最大值。 三个内角
三个内角 的对边分别为
的对边分别为 ,向量
,向量 ,
,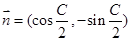 ,且
,且 与
与 的夹角为
的夹角为 .
. 的值;
的值; ,
, ,求
,求 的值.
的值. 的三个内角
的三个内角 所对的边分别为
所对的边分别为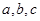 ,
,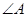 是锐角,且
是锐角,且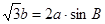 .
.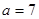 ,
,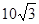 ,求
,求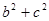 的值.
的值.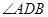 =750,
=750,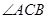 ="30°,AD" =
="30°,AD" =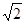 .
. 的图象与
的图象与 轴相邻两交点的距离为
轴相邻两交点的距离为 。
。 的值;
的值; 分别是角A,B,C的对边,且
分别是角A,B,C的对边,且 求
求 的取值范围。
的取值范围。