题目内容
向量 ,
,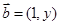 ,已知
,已知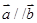 ,且有函数
,且有函数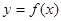 .
.
(1)求函数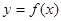 的周期;
的周期;
(2)已知锐角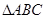 的三个内角分别为
的三个内角分别为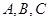 ,若有
,若有 ,边
,边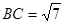 ,
,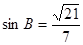 ,求
,求 的长及
的长及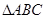 的面积.
的面积.
(1)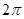 ;(2)
;(2)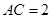 ,
,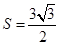 .
.
解析试题分析:(1)利用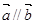 的充要条件得出
的充要条件得出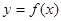 ,再化简成
,再化简成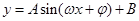 类型求周期;(2)先由条件
类型求周期;(2)先由条件 求出角
求出角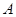 ,再由正弦定理
,再由正弦定理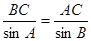 求
求 ,然后只需求出
,然后只需求出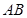 或
或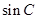 即可求
即可求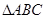 的面积.
的面积.
试题解析:解:由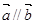 得
得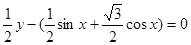 3分
3分
即 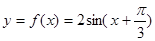 5分
5分
(1)函数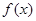 的周期为
的周期为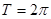 6分
6分
(2)由 得
得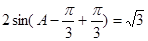 即
即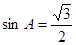
∵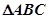 是锐角三角形∴
是锐角三角形∴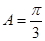 8分
8分
由正弦定理: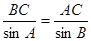 及条件
及条件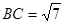 ,
,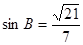
得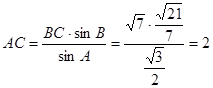 , 10分
, 10分
又∵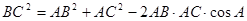
即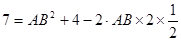 解得
解得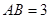 11分
11分
∴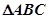 的面积
的面积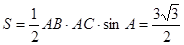 12分
12分
考点:1、平面向量与三角函数结合,2、正弦定理与余弦定理综合运用,3、三角形面积公式.

练习册系列答案
相关题目
 中的内角
中的内角 、
、 、
、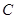 所对的边分别为
所对的边分别为 、
、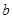 、
、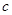 ,若
,若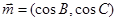 ,
,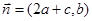 ,且
,且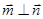 .
.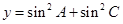 的取值范围.
的取值范围.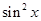 -sin(2x-
-sin(2x-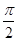 ).
).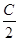 )=
)= ,若sinB=2sinA,求△ABC的面积.
,若sinB=2sinA,求△ABC的面积. 三个内角
三个内角 的对边分别为
的对边分别为 ,向量
,向量 ,
,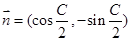 ,且
,且 与
与 的夹角为
的夹角为 .
. 的值;
的值; ,
, ,求
,求 的值.
的值. 的三个内角
的三个内角 所对的边分别为
所对的边分别为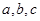 ,
,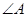 是锐角,且
是锐角,且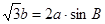 .
.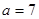 ,
,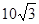 ,求
,求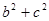 的值.
的值.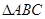 中,
中,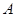 、
、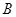 、
、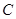 所对的边分别为
所对的边分别为 、
、 、
、 .已知向量
.已知向量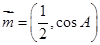 ,
,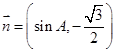 ,且
,且 .
. ,
,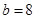 ,求
,求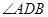 =750,
=750,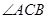 ="30°,AD" =
="30°,AD" =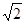 .
.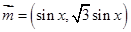 ,
, ,设函数
,设函数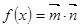 .
. 的解析式,并求
的解析式,并求 上的最小值;
上的最小值; 中,
中, 分别是角
分别是角 的对边,
的对边, 为锐角,若
为锐角,若 ,
, ,
, ,求
,求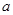 .
.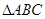 的角A、B、C所对的边分别为
的角A、B、C所对的边分别为 ,已知
,已知