题目内容
在边长为1的正△ABC中，若
=
，
=
，
=
，则
•
+
•
+
•
=（ ）
| AB |
| a |
| BC |
| b |
| CA |
| c |
| a |
| b |
| b |
| c |
| c |
| a |
A、
| ||
B、-
| ||
| C、3 | ||
| D、0 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：根据向量的数量积的运算解答，注意向量的夹角不一定是三角形的内角．
解答：
解：∵在边长为1的正△ABC中，若
=
，
=
，
=
，
∴
•
+
•
+
•
=AB×BC×cos120°+BC×AC×cos120°+AC×AB×cos20°=-
-
-
=-
；
故选B．
| AB |
| a |
| BC |
| b |
| CA |
| c |
∴
| a |
| b |
| b |
| c |
| c |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
故选B．
点评：本题考查了向量的数量积的应用；特别注意三角形的内角不一定是向量的夹角；当向量共起点或者共终点时，向量的夹角才是对应线段的内角．
练习册系列答案
相关题目
若定义在R上的f（x）满足f（x+1）=
，则函数f（x）必有一周期为（ ）
| 1+f(x) |
| 1-f(x) |
| A、2 | B、3 | C、4 | D、5 |
已知A，B，C为三角形的三个内角，它们的对边长分别为a，b，c，已知直线xsinA+ysinB+sinC=0到原点的距离大于1，则此三角形为（ ）
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、不能确定 |
已知抛物线的方程为y2=2x，则其焦点坐标为（ ）
A、(0，
| ||
B、(
| ||
C、(±
| ||
D、(0，-
|
随机变量x的分布列P（x=k）=
（k=1，2，3，4），其中P为常数，则P（
＜x＜
）=（ ）
| P |
| k(k+1) |
| 1 |
| 2 |
| 5 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=
（a＞1）的图象的大致形状是（ ）
| |x| |
| xax |
A、 |
B、 |
C、 |
D、 |
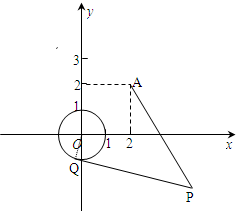如图，已知⊙O：x2+y2=1和定点A（2，2），由⊙O外一点P（a，b）向⊙O引切线PQ，Q为切点，且满足|PQ|=|PA|．