题目内容
7．若直线x+2y+1=0与直线mx+y-2=0互相平行，则m的值为（ ）| A． | 1 | B． | $\frac{1}{2}$ | C． | -2 | D． | $-\frac{2}{3}$ |
分析 利用两条直线平行，它们的斜率相等或斜率都不存在的性质求解．
解答 解：∵直线x+2y+1=0与直线mx+y-2=0互相平行，
∴-$\frac{1}{2}$=-m，
∴m=$\frac{1}{2}$，
故选：B．
点评 本题考查实数值的求法，是基础题，解题时要注意直线与直线平行的性质的合理运用．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
12．已知l1：mx+y-2=0，l2：（m+1）x-2my+1=0，若l1⊥l2则m=（ ）
| A． | m=0 | B． | m=1 | C． | m=0或m=1 | D． | m=0或m=-1 |
16．已知向量$\overrightarrow a=（cosx-sinx，2cosx）$，$\overrightarrow b=（cosx+sinx，sinx）（x∈R）$，则函数$f（x）={（\overrightarrow a•\overrightarrow b）^2}-1$是（ ）
| A． | 周期为π的偶函数 | B． | 周期为π的奇函数 | ||
| C． | 周期为$\frac{π}{2}$的偶函数 | D． | 周期为$\frac{π}{2}$的奇函数 |
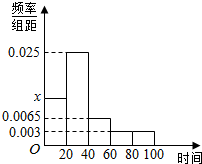某学校随机调查了部分学生的上学所需时间（单位：分钟），并将所得数据绘制成频率分布直方图（如图），其中，上学所需时间的范围是[0，100]，样本数据分组为[0，20），[20，40），[40，60），[60，80），[80，100]