题目内容
1.若x,y满足$\left\{\begin{array}{l}{x-y≤0}\\{x+y-1≤0}\\{x≥0}\\{\;}\end{array}\right.$,则z=5x-3y+1的最小值为( )| A. | -2 | B. | 0 | C. | 1 | D. | 3 |
分析 作出不等式组对应的平面区域,利用z的几何意义,即可得到结论.
解答  解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
由z=5x-3y+1得y=$\frac{5}{3}$x+$\frac{1-z}{3}$,
平移直线y=$\frac{5}{3}$x+$\frac{1-z}{3}$,
由图象可知当直线y=$\frac{5}{3}$x+$\frac{1-z}{3}$经过点A(0,1)时,直线的截距最大,
此时z最小,
此时z=-3+1=-2,
故选:A.
点评 本题主要考查导数的几何意义,以及利用线性规划的应用,综合性较强,考查学生解决问题的能力.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
9.已知函数f(x)=$\left\{\begin{array}{l}|lo{g}_{3}x|,0<x<3\\-cos(\frac{π}{3}x),3≤x≤9\end{array}\right.$,若存在实数x1,x2,x3,x4,当x1<x2<x3<x4时满足f(x1)=f(x2)=f(x3)=f(x4),则x1•x2•x3•x4的取值范围是( )
| A. | (7,$\frac{29}{4}$) | B. | (21,$\frac{135}{4}$) | C. | [27,30) | D. | (27,$\frac{135}{4}$) |
6.已知集合A={-1,0,1,},B={x|(x-1)2<1},则A∩B=( )
| A. | {-1,0,1} | B. | {0} | C. | {1} | D. | ∅ |
10.下列有关命题的说法错误的是( )
| A. | 函数f(x)=sinxcosx的最小正周期为π | |
| B. | 函数$f(x)=lnx+\frac{1}{2}x-2$在区间(2,3)内有零点 | |
| C. | 已知函数$f(x)={log_a}({x^2}-2x+2)$,若$f(\frac{1}{2})>0$,则0<a<1 | |
| D. | 在某项测量中,测量结果ξ服从正态分布N(2,σ2)(σ>0).若ξ在(-∞,1)内取值的概率为0.1,则ξ在(2,3)内取值的概率为0.4 |
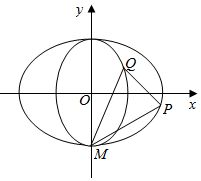 如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0)过点M(0,-$\sqrt{2}$),离心率为$\frac{\sqrt{2}}{2}$.
如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0)过点M(0,-$\sqrt{2}$),离心率为$\frac{\sqrt{2}}{2}$.