题目内容
如果数列 {an}满足
-
=1,a1=1,则 a2015= .
| 1 |
| an+1 |
| 1 |
| an |
考点:数列递推式
专题:等差数列与等比数列
分析:由已知得{
}是首项为1,公差为1的等差数列,从而
=n,进而an=
,由此能求出a2015.
| 1 |
| an |
| 1 |
| an |
| 1 |
| n |
解答:
解:∵{an}满足
-
=1,a1=1,
∴
=1,∴{
}是首项为1,公差为1的等差数列,
∴
=1+(n-1)×1=n,
∴an=
,
∴a2015=
.
故答案为:
.
| 1 |
| an+1 |
| 1 |
| an |
∴
| 1 |
| a1 |
| 1 |
| an |
∴
| 1 |
| an |
∴an=
| 1 |
| n |
∴a2015=
| 1 |
| 2015 |
故答案为:
| 1 |
| 2015 |
点评:本题考查数列的通项公式的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
设{an}是等差数列,若log2a7=3,则a6+a8等于( )
| A、6 | B、8 | C、9 | D、16 |
如图所示是一个几何体的三视图,则该几何体的表面积为( )


| A、12+4π |
| B、20+6π |
| C、12+6π |
| D、16+4π |
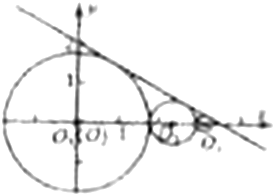 设O1,O2,…,On,…是坐标平面上圆心在x轴非负半轴上的一列圆(其中O1为坐标原点),且圆On和圆On+1相外切,并均与直线x+
设O1,O2,…,On,…是坐标平面上圆心在x轴非负半轴上的一列圆(其中O1为坐标原点),且圆On和圆On+1相外切,并均与直线x+