题目内容
已知函数f(x)=
,则方程2f(x)=1的根的个数为( )
|
| A、1 | B、2 | C、3 | D、4 |
考点:利用导数研究函数的极值,根的存在性及根的个数判断
专题:函数的性质及应用,导数的综合应用
分析:根据解析式利用导数判断在(-∞,-1)(1,+∞)单调递增,(-1,1)单调递减,极大值f(-1)=4,极小值f(1)=0,画出图象可判断答案.求出
解答:
解:∵函数f(x)=
,
∴x∈[1,+∞)单调递增,
f(1)=1-1=0,
当x<1时,f(x)=x3-3x+2,
f′(x)=3x2-3,x<1,
f′(x)=3x2-3=0,x=±1,
f′(x)=3x2-3>0,x>1(舍去),x<-1,
f′(x)=3x2-3<0,-1<x<1,
∴在(-∞,-1)(1,+∞)单调递增,(-1,1)单调递减,
极大值f(-1)=4,极小值f(1)=0,
∴f(x)=
,
f(x)与y=
交点3个,
∴方程2f(x)=1的根的个数为3,
故选:C

|
∴x∈[1,+∞)单调递增,
f(1)=1-1=0,
当x<1时,f(x)=x3-3x+2,
f′(x)=3x2-3,x<1,
f′(x)=3x2-3=0,x=±1,
f′(x)=3x2-3>0,x>1(舍去),x<-1,
f′(x)=3x2-3<0,-1<x<1,
∴在(-∞,-1)(1,+∞)单调递增,(-1,1)单调递减,
极大值f(-1)=4,极小值f(1)=0,
∴f(x)=
| 1 |
| 2 |
f(x)与y=
| 1 |
| 2 |
∴方程2f(x)=1的根的个数为3,
故选:C

点评:本题考查了运用导数判断函数的单调性,极值,结合图象判断函数交点个数,方程的根的问题,属于中档题.

练习册系列答案
相关题目
不等式
<0成立的一个充分不必要条件是( )
| 1-x |
| x |
| A、x>1 | B、x<0或x>1 |
| C、0<x<1 | D、x≤0 |
将函数y=3sin(2x-
)的图象经过( )变换,可以得到函数y=3sin2x的图象.
| π |
| 4 |
A、沿x轴向右平移
| ||
B、沿x轴向左平移
| ||
C、沿x轴向右平移
| ||
D、沿x轴向左平移
|
若a<b<0,则下列不等式成立的是( )
| A、ac<bc<0 | ||||
B、
| ||||
C、
| ||||
| D、a2>b2 |
在△ABC中,tan
=2sinC,若AB=1,求△ABC周长的取值范围( )
| A+B |
| 2 |
| A、(2,3] |
| B、[1,3] |
| C、(0,2] |
| D、(2,5] |
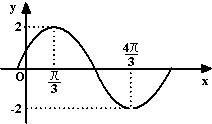 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<